题目内容
12.若三角形三内角的度数之比为1:2:3,最大边的长是16cm,则最小边的长是8cm.分析 根据三角形的内角和等于180°求出最大角和最小角,然后根据直角三角形30°角所对的直角边等于斜边的一半解答.
解答 解:∵三角形三内角的度数之比为1:2:3,
∴三角形的最大的内角度数是:180°×$\frac{3}{1+2+3}$=90°,
最小的内角度数是:180°×$\frac{1}{1+2+3}$=30°,
∴此三角形是有一个锐角是30°的直角三角形,
∵最大边的长是16cm,
∴则最小边的长是16×$\frac{1}{2}$=8cm.
故答案为:8cm.
点评 本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,三角形的内角和定理,熟记性质并求出此三角形是有一个锐角是30°的直角三角形是解题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
3.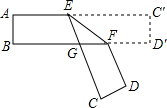 如图,把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°,则下列结论正确的有( )
如图,把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°,则下列结论正确的有( )
(1)∠C′EF=32°(2)∠AEC=116°(3)∠BGE=64° (4)∠BFD=116°.
 如图,把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°,则下列结论正确的有( )
如图,把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°,则下列结论正确的有( )(1)∠C′EF=32°(2)∠AEC=116°(3)∠BGE=64° (4)∠BFD=116°.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.已知x1、x2是一元二次方程x2-4x+1=0的两个根,则x1•x2等于( )
| A. | -4 | B. | -1 | C. | 1 | D. | 4 |
2.如果零上3℃记作+3℃,那么零下2℃记作( )
| A. | -2℃ | B. | -3℃ | C. | +3℃ | D. | +2℃ |
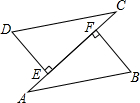 如图所示,已知AB=CD,DE⊥AC,BF⊥AC,E、F为垂足,DE=BF,试说明AE与CF相等.
如图所示,已知AB=CD,DE⊥AC,BF⊥AC,E、F为垂足,DE=BF,试说明AE与CF相等.