题目内容
15.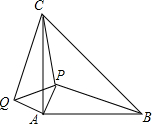 如图,在等腰三角形ABC中,∠CAB=90°,P是△ABC内一点,PA=1,PB=3,PC=$\sqrt{7}$,将△APB绕点A逆时针旋转后与△AQC重合.求:
如图,在等腰三角形ABC中,∠CAB=90°,P是△ABC内一点,PA=1,PB=3,PC=$\sqrt{7}$,将△APB绕点A逆时针旋转后与△AQC重合.求:(1)线段PQ的长;
(2)∠APC的度数.
分析 (1)由旋转的性质可知△QPA为等腰直角三角形,利用勾股定理可求得QP的长;
(2)△QPA为等腰直角三角形,故此∠APQ=45°,在△QPC中PC=$\sqrt{7}$,QC=3,QP=$\sqrt{2}$,由勾股定理的逆定理可证△QCP为直角三角形,从而可求得∠APC=135°.
解答 解:(1)∵△APB绕点A旋转与△AQC重合
∴AQ=AP=1,∠QAP=∠CAB=90°.
在Rt△APQ中,由勾股定理得:PQ=$\sqrt{A{Q^2}+A{P^2}}$=$\sqrt{{1^2}+{1^2}}$=$\sqrt{2}$.
(2)∵∠QAP=90°,AQ=AP,
∴∠APQ=45°.
∵△APB绕点A旋转与△AQC重合,
∴CQ=BP=3.
∵在△CPQ中PQ=$\sqrt{2}$,CQ=3,CP=$\sqrt{7}$,
∴CP2+PQ2=($\sqrt{7}$)2+($\sqrt{2}$)2=9,CQ2=32=9.
∴CP2+PQ2=CQ2.
∴∠CPQ=90°.
∴∠APC=∠CPQ+∠APQ=135°.
点评 本题主要考查的是旋转的性质、勾股定理的逆定理的应用,证得△QCP为直角三角形是解题的关键.

练习册系列答案
相关题目
5.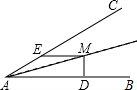 如图,∠BAC=30°,AM是∠BAC的平分线,过M作ME∥BA 交AC于E,作MD⊥BA,垂足为D,ME=10cm,则MD的长( )
如图,∠BAC=30°,AM是∠BAC的平分线,过M作ME∥BA 交AC于E,作MD⊥BA,垂足为D,ME=10cm,则MD的长( )
 如图,∠BAC=30°,AM是∠BAC的平分线,过M作ME∥BA 交AC于E,作MD⊥BA,垂足为D,ME=10cm,则MD的长( )
如图,∠BAC=30°,AM是∠BAC的平分线,过M作ME∥BA 交AC于E,作MD⊥BA,垂足为D,ME=10cm,则MD的长( )| A. | 10cm | B. | 5cm | C. | 3cm | D. | 7cm |
3.若两个有理数的和为负数,那么这两个有理数( )
| A. | 一定是负数 | B. | 一正一负,且负数的绝对值大 | ||
| C. | 一个为零,另一个为负数 | D. | 至少有一个是负数 |
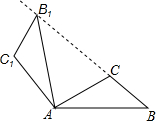 如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小是80度.
如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小是80度.