题目内容
10.在△ABC中,过点A作AD⊥AB交BC于点D,过点A作AF⊥AC交BC于点F,在AB上取点E,使得AD=AE,过点E作EG⊥AB交AF延长线于点G.(1)如图1,当∠CAD=30°,AD=2时,求△AEG的面积;
(2)如图2,当AF=AE时,求证:AG+EG=AB.
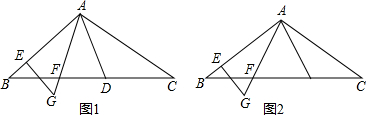
分析 (1)首先证明∠EAG=∠CAD=30°,在Rt△AEG中,解直角三角形即可解决问题;
(2)以A为圆心AB为半径作⊙A,延长AG交⊙A于H,连接EH交BC于O.只要证明GE=GH即可解决问题;
解答 解:(1)如图1中,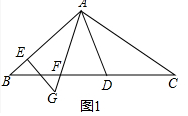
∵AD⊥AB,AF⊥AC,
∴∠BAD=∠CAF=90°,
∴∠EAG=∠CAD=30°,
∵EG⊥AB,
∴∠AEG=90°,
∵AD=AE=2,
∴EG=$\frac{\sqrt{3}}{3}$AE=$\frac{2\sqrt{3}}{3}$,
∴△AEG的面积=$\frac{1}{2}$AE•EG=$\frac{1}{2}×$2×$\frac{2\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$;
(2)以A为圆心AB为半径作⊙A,延长AG交⊙A于H,连接EH交BC于O.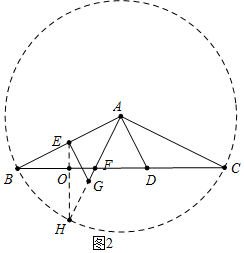
∵AE=AF,∠EAH=∠FAB,AH=AB,
∴△EAH≌△FAB,
∴∠B=∠H,
∵∠BAD=∠CAF=90°,
∴∠BAG=∠CAD,
∵AF=AD=AE,
∴∠AFD=∠ADF,
∴∠B+∠BAF=∠C+∠DAC,
∴∠B=∠C=∠H,
∵∠CFA=∠HFO,
∴∠HOF=∠CAF=90°,
∵EG⊥AB,
∴∠BEG=90°,
∵∠GEH+∠BEH=90°,∠BEH+∠B=90°,
∴∠B=∠GEH=∠H,
∴EG=GH,
∴AG+GE=AG+GH=AH=AB,
∴AG+EG=AB.
点评 本题考查全等三角形的判定和性质、等腰三角形的判定和性质、圆的有关知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
15.下列四个实数中,最小的实数是( )
| A. | $\sqrt{2}$ | B. | -1 | C. | -3 | D. | 0 |
 如图,CA⊥AB,垂足为A,AB=24,AC=12,射线BM⊥AB,垂足为B,一动点E从A点出发以3厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过0,4,12,16秒时,△DEB与△BCA全等.
如图,CA⊥AB,垂足为A,AB=24,AC=12,射线BM⊥AB,垂足为B,一动点E从A点出发以3厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过0,4,12,16秒时,△DEB与△BCA全等.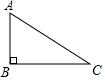 如图,Rt△ABC中,∠ABC=90°,AB=3,BC=6,以AB为边作△ABD,使△ABD与△ABC相似,则在△ABC所在的平面内共存在这样的点D(不与C重合)共有( )
如图,Rt△ABC中,∠ABC=90°,AB=3,BC=6,以AB为边作△ABD,使△ABD与△ABC相似,则在△ABC所在的平面内共存在这样的点D(不与C重合)共有( ) 如图,∠ABC=∠ACB,BD、CD、BE分别平分△ABC的内角∠ABC、外角∠ACP、外角∠MBC,以下结论:①AD∥BC;②DB⊥BE;③∠BDC+∠ABC=90°;④∠A+2∠BEC=180°;⑤DB平分∠ADC.其中正确的结论有:①②③④(填序号)
如图,∠ABC=∠ACB,BD、CD、BE分别平分△ABC的内角∠ABC、外角∠ACP、外角∠MBC,以下结论:①AD∥BC;②DB⊥BE;③∠BDC+∠ABC=90°;④∠A+2∠BEC=180°;⑤DB平分∠ADC.其中正确的结论有:①②③④(填序号)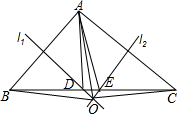 如图,在△ABC中,AB边的垂直平分线l1,交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,△ADE的周长为6,△OBC的周长为16,则AO的长为5.
如图,在△ABC中,AB边的垂直平分线l1,交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,△ADE的周长为6,△OBC的周长为16,则AO的长为5.