题目内容
平面直角坐标系中，A（-4，-2），B（0，-2），点C在x轴的正半轴，以O、B、C为顶点的三角形与△ABO相似，则点C的坐标是 ．
考点：相似三角形的判定,坐标与图形性质
专题：
分析：求出AB和OB的值，根据相似三角形的判定定理得出当
=
或
=
时，以O、B、C为顶点的三角形与△ABO相似，代入求出OC，即可得出答案．
| OB |
| OC |
| AB |
| OB |
| OC |
| OB |
| AB |
| OB |
解答：解：∵A（-4，-2），B（0，-2），
∴AB=4，OB=2，∠ABO=90°，
∴
=2，
∵∠BOC=90°，
∴当
=
或
=
时，以O、B、C为顶点的三角形与△ABO相似，
∴OC=1或4，
∴点C的坐标是（1，0）或（4，0），
故答案为：（1，0）或（4，0）．
∴AB=4，OB=2，∠ABO=90°，
∴
| AB |
| OB |
∵∠BOC=90°，
∴当
| OB |
| OC |
| AB |
| OB |
| OC |
| OB |
| AB |
| OB |
∴OC=1或4，
∴点C的坐标是（1，0）或（4，0），
故答案为：（1，0）或（4，0）．
点评：本题考查了相似的三角形的判定定理的应用，能正确运用判定定理得出当
=
或
=
时，以O、B、C为顶点的三角形与△ABO相似是解此题的关键．
| OB |
| OC |
| AB |
| OB |
| OC |
| OB |
| AB |
| OB |
练习册系列答案
阅读快车系列答案
相关题目
如图，将边长为6cm的正方形ABCD折叠，使点D落在AB边的中点E处，折痕为FH，点C落在Q处，EQ与BC交于点G，求△EBG的周长．
某市承办一项大型比赛，在市内有三个体育馆承接所有比赛，现要修建一个运动员公寓，使得运动员公寓到三个体育馆的距离相等，若三个体育馆的位置如图所示，那么运动员公寓应建立在何处？
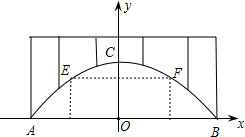廊桥是我国古老的文化遗产，如图，是某座抛物线型的廊桥示意图，以水面AB所在直线为x轴，AB中点O为原点，建立平面直角坐标系．已知水面AB宽40米，抛物线最高点C到水面AB的距离为10米，为保护廊桥的安全，在该抛物线上距水面AB高为8米的点E，F处要安装两盏警示灯，求这两盏灯的水平距离EF．（结果保留根号）
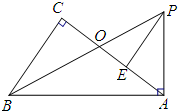如图，在△ABC中，∠C=90°，△BAP中，∠BAP=90°，已知∠CBO=∠ABP，BP交AC于点O，E为AC上一点，且AE=OC．