题目内容
8.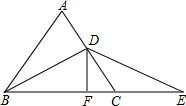 已知,如图,△ABC是等边三角形,BD是AC边上的高,延长BC到E,使CE=CD,过D作DF⊥BE于F.
已知,如图,△ABC是等边三角形,BD是AC边上的高,延长BC到E,使CE=CD,过D作DF⊥BE于F.(1)求证:BD=DE;
(2)请猜想FC与BF间的数量关系,并证明.
分析 (1)因为△ABC是等边三角形,所以∠ABC=∠ACB=60°,BD是AC边上的高,则∠DBC=30°,再由题中条件求出∠E=30°,即可判断△BDE的形状.
(2)根据30°所对的直角边等于斜边的一半,得出DC=2FC,BC=2DC,从而证得BF=3FC.
解答 (1)证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵BD⊥AC,
∴AD=CD,∠DBC=$\frac{1}{2}$∠ABC=30°,
∵CE=CD,
∴∠CDE=∠E,
∵∠ACB=∠CDE+∠E,
∴∠E=30°,
∴∠DBE=∠E,
∴BD=DE;
(2)BF=3FC;
证明:∵DF⊥BE,∠BCD=60°,
∴DC=2FC,
∵BD⊥AC,∠DBC=30°,
∴BC=2DC,
∴BC=4FC,
∴BF=3FC.
点评 本题考查了等边三角形的性质,等腰三角形的性质,三角形外角的性质,30°所对的直角边等于斜边的一半的性质,熟练掌握这些性质是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
18.下面几个有理数最大的是( )
| A. | 2 | B. | 0 | C. | -3 | D. | -1 |
19. 2015年3月全国两会期间,民生活题成为了社会关注的焦点,成都商报为了了解百姓“两会民生活题”的聚焦点,记者随机调查了成都市部分市民,并对调查进行整理,绘制成了如图所示的不完整的统计图表.
2015年3月全国两会期间,民生活题成为了社会关注的焦点,成都商报为了了解百姓“两会民生活题”的聚焦点,记者随机调查了成都市部分市民,并对调查进行整理,绘制成了如图所示的不完整的统计图表.
根据图表中提供的信息可得统计表中m=40,n=100,扇形统计图中D组所占的百分比为25%.
 2015年3月全国两会期间,民生活题成为了社会关注的焦点,成都商报为了了解百姓“两会民生活题”的聚焦点,记者随机调查了成都市部分市民,并对调查进行整理,绘制成了如图所示的不完整的统计图表.
2015年3月全国两会期间,民生活题成为了社会关注的焦点,成都商报为了了解百姓“两会民生活题”的聚焦点,记者随机调查了成都市部分市民,并对调查进行整理,绘制成了如图所示的不完整的统计图表.| 组别 | 焦点话题 | 频数(人数) |
| A | 延迟退休 | 120 |
| B | 汽车尾号限行 | 80 |
| C | 就业养老 | m |
| D | 教育医疗 | n |
| E | 生态环保 | 60 |
3.已知菱形ABCD的边长为5,中心为O,且OA,OB的长是关于x的方程x2+(2m+1)x+m2-4=0的两个实数根,则m的值为( )
| A. | -4 | B. | 2 | C. | -4或2 | D. | 以上都不对 |
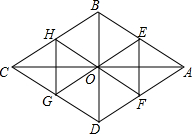 如图,四边形ABCD是菱形,对角线AC=8,BD=6,E,F分别是AB,AD的中点,连接EO并延长交CD于G点,连接FO并延长交CB于H点,△OEF与△OGH组成的图形称为蝶形,则蝶形的周长为16.
如图,四边形ABCD是菱形,对角线AC=8,BD=6,E,F分别是AB,AD的中点,连接EO并延长交CD于G点,连接FO并延长交CB于H点,△OEF与△OGH组成的图形称为蝶形,则蝶形的周长为16.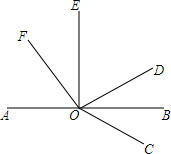 如图.点O是直线AB上一点,∠AOE是直角,∠FOD=90°,OB平分∠DOC.
如图.点O是直线AB上一点,∠AOE是直角,∠FOD=90°,OB平分∠DOC.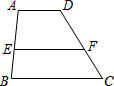 四边形ABCD中,E、F分别为AB、CD上的点,且AD∥EF∥BC,AE:EB=3:2,AD=2cm,BC=4cm,则EF=$\frac{16}{5}$cm.
四边形ABCD中,E、F分别为AB、CD上的点,且AD∥EF∥BC,AE:EB=3:2,AD=2cm,BC=4cm,则EF=$\frac{16}{5}$cm.