题目内容
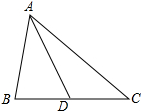如图所示，AD是△ABC的边BC的中线．（1）画出以点D为对称中心，与△ABD成中心对称的三角形；
（2）若AB=10，AC=12，求AD长的取值范围．
考点：作图-旋转变换
专题：
分析：（1）利用关于点对称图形的性质得出对应点位置进而得出答案；
（2）利用三角形三边关系得出答案．
（2）利用三角形三边关系得出答案．
解答：
解：（1）如图所示：△CDE即为所求；
（2）∵△CDE与△ABD成中心对称，
∴AB=EC=10，AD=DE，
∴AC-EC＜AE＜AC+EC
∴2＜AE＜22，
∴1＜AD＜11．
解：（1）如图所示：△CDE即为所求；（2）∵△CDE与△ABD成中心对称，
∴AB=EC=10，AD=DE，
∴AC-EC＜AE＜AC+EC
∴2＜AE＜22，
∴1＜AD＜11．
点评：此题主要考查了旋转变换以及三角形三边关系，熟练利用关于点对称图形的性质得出是解题关键．
练习册系列答案
相关题目
如图，在△AFC中，B点为AC的中点，E为BD的中点，连接DE、AE，AE交CD于点F，则AF：AE=
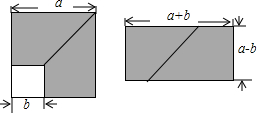如图的分割正方形，拼接成长方形方案中，可以验证（ ）| A、（a+b）2=a2+2ab+b2 |
| B、（a-b）2=a2-2ab+b2 |
| C、（a+b）2=（a+b）2-4ab |
| D、（a+b）（a-b）=a2-b2 |
两个有理数a、b在数轴上的位置如图所示，则a+b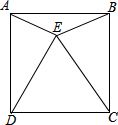
如图所示，E为正方形ABCD内一点，且△EDC是等边三角形，求∠EAD的度数．