题目内容
意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长值构造正方形,再分别依次从左到右取2个、3个、4个、5个…正方形拼成如上长方形,若按此规律继续作长方形,则序号为⑦的长方形周长是 .


考点:规律型:图形的变化类
专题:
分析:根据图示规律,依次写出相应序号的矩形的宽与长,便不难发现,下一个矩形的宽是上一个矩形的长,长是上一个矩形的长与宽的和,然后写到序号为⑧的矩形宽与长,再根据矩形的周长公式计算即可得解.
解答:解:由图可知,序号为①的矩形的宽为1,长为2,
序号为②的矩形的宽为2,长为3,3=1+2,
序号为③的矩形的宽为3,长为5,5=2+3,
序号为④的矩形的宽为5,长为8,8=3+5,
序号为⑤的矩形的宽为8,长为13,13=5+8,
序号为⑥的矩形的宽为13,长为21,21=8+13,
序号为⑦的矩形的宽为21,长为34,34=13+21,
所以,序号为⑦的矩形周长=2(34+21)=2×55=110.
故答案为:110.
序号为②的矩形的宽为2,长为3,3=1+2,
序号为③的矩形的宽为3,长为5,5=2+3,
序号为④的矩形的宽为5,长为8,8=3+5,
序号为⑤的矩形的宽为8,长为13,13=5+8,
序号为⑥的矩形的宽为13,长为21,21=8+13,
序号为⑦的矩形的宽为21,长为34,34=13+21,
所以,序号为⑦的矩形周长=2(34+21)=2×55=110.
故答案为:110.
点评:考查了图形的变化类问题,要想得到长方形的周长规律,应先找长方形长、宽的变换规律.分析图形中的长和宽,然后结合图表中长方形的周长即可得出长方形周长的变换规律.

练习册系列答案
相关题目
在△ABC中,若∠A,∠B都是锐角,则△ABC是( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、以上都有可能 |
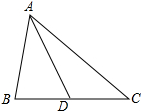 如图所示,AD是△ABC的边BC的中线.
如图所示,AD是△ABC的边BC的中线.
 如图,在△ABC中,AB=AC,BD=CD,AD=AE,∠BAD=40°,∠CDE=
如图,在△ABC中,AB=AC,BD=CD,AD=AE,∠BAD=40°,∠CDE=