题目内容
已知a2+b2-a+4b+4
=0,求代数式a2+b2的值.
| 1 |
| 4 |
考点:配方法的应用,非负数的性质:偶次方
专题:
分析:将a2+b2-a+4b+4
=0配方成(a-
)2+(b+2)2=0的形式求得a、b后即可求得代数式的值.
| 1 |
| 4 |
| 1 |
| 2 |
解答:解:∵a2+b2-a+4b+4
=0,
∴a2-a+
+b2+4b+4=0,
∴(a-
)2+(b+2)2=0,
∴a=
,b=-2,
∴a2+b2=
+4=4
.
| 1 |
| 4 |
∴a2-a+
| 1 |
| 4 |
∴(a-
| 1 |
| 2 |
∴a=
| 1 |
| 2 |
∴a2+b2=
| 1 |
| 4 |
| 1 |
| 4 |
点评:本题考查了配方法的应用及非负数的性质,解题的关键是配方,难度不大.

练习册系列答案
相关题目
 两个长方形重叠部分的面积相当于大长方形的
两个长方形重叠部分的面积相当于大长方形的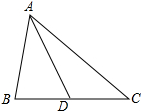 如图所示,AD是△ABC的边BC的中线.
如图所示,AD是△ABC的边BC的中线.