题目内容
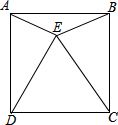 如图所示,E为正方形ABCD内一点,且△EDC是等边三角形,求∠EAD的度数.
如图所示,E为正方形ABCD内一点,且△EDC是等边三角形,求∠EAD的度数.考点:正方形的性质,全等三角形的判定与性质
专题:
分析:由E为正方形ABCD内一点,且△EDC是等边三角形,易证得△ADE是等腰三角形,且AD=DE,易求得∠ADE=∠ADC-∠EDC=30°,继而求得答案.
解答:解:∵E为正方形ABCD内一点,且△EDC是等边三角形,
∴∠ADC=90°,∠EDC=60°,AD=CD=ED,
∴∠ADE=∠ADC-∠EDC=30°,
∴∠EAD=∠AED=
=75°.
∴∠ADC=90°,∠EDC=60°,AD=CD=ED,
∴∠ADE=∠ADC-∠EDC=30°,
∴∠EAD=∠AED=
| 180°-∠ADE |
| 2 |
点评:此题考查了正方形的性质以及等边三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
若函数y=axa2-2是二次函数且图象开口向上,则a=( )
| A、-2 | B、2 | C、2或-2 | D、1 |
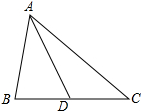 如图所示,AD是△ABC的边BC的中线.
如图所示,AD是△ABC的边BC的中线. 如图,在△ABC中,AB=AC,BD=CD,AD=AE,∠BAD=40°,∠CDE=
如图,在△ABC中,AB=AC,BD=CD,AD=AE,∠BAD=40°,∠CDE=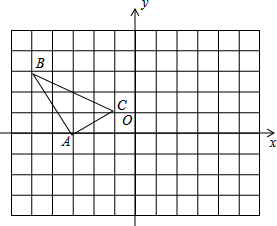 在正方形网格中每个小正方形边长都是1个单位,如图建立直角坐标系,△ABC在坐标系中位置如图所示
在正方形网格中每个小正方形边长都是1个单位,如图建立直角坐标系,△ABC在坐标系中位置如图所示