题目内容
4.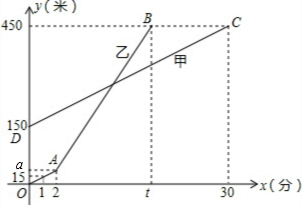 甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,请根据图象提供的信息解答下列问题:
甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,请根据图象提供的信息解答下列问题:(1)甲登山的速度是每分钟10米,乙在A处提速时距地面的高度a为30 米.
(2)若乙提速后,乙的速度是甲登山速度的3倍,请分别写出甲登山过程及乙在AB段登山时距地面的高度y(米)与登山时间x(分)之间的函数关系式.
(3)登山多长时间时,乙追上了甲?
分析 (1)甲的速度=(450-150)÷30=10,根据图象知道乙一分的时间,走了15米,然后即可求出A地提速时距地面的高度;
(2)乙提速后,乙的速度是甲登山速度的3倍,所以乙的速度是30米/分.那么求出点B的坐标,加上点A的坐标代入一次函数解析式即可求出乙的函数解析式,把C、D坐标代入一次函数解析式可求出甲的函数解析式;
(3)乙追上了甲即此时的y的值相等,然后求出时间在计算距A地的高度.
解答 解:(1)甲的速度为:(450-150)÷30=10米/分,
根据图中信息知道乙一分的时间,走了15米,
那么2分时,将走30米;
(2)由图知:x=$\frac{450-30}{30}$+2=16,
∵C(30,450),D(0,150)
∴线段CD的解析式:y甲=10x+150(0≤x≤30);
∵A(2,30),B(16,450),
∴折线OAB的解析式为:y乙=$\left\{\begin{array}{l}{15x(0≤x≤2)}\\{30x-30(2≤x≤16)}\end{array}\right.$;
(3)由$\left\{\begin{array}{l}{y=10x+150}\\{y=30x-30}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=9}\\{y=240}\end{array}\right.$,
∴登山9分钟时乙追上甲.
点评 本题主要考查用待定系数法求一次函数关系式,并会用一次函数研究实际问题,关键是正确理解题意.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
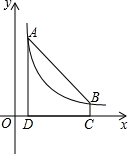 如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
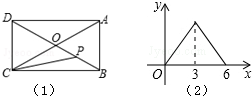 如图(1),矩形ABCD的两条对角线相交于点O,∠BOC=120°,AB=3,一动点P以均匀的速度沿折线OB-BA运动,若点P的运动时间x(s)与点C、O、P围成的三角形的面积y之间的函数图象如图(2),那么P点运动的速度为1.
如图(1),矩形ABCD的两条对角线相交于点O,∠BOC=120°,AB=3,一动点P以均匀的速度沿折线OB-BA运动,若点P的运动时间x(s)与点C、O、P围成的三角形的面积y之间的函数图象如图(2),那么P点运动的速度为1.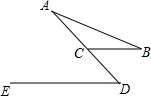 如图已知,BC∥DE,∠A=26°,∠B=34°,求∠D的度数.
如图已知,BC∥DE,∠A=26°,∠B=34°,求∠D的度数.