题目内容
已知函数y=（x-n）（x-3）与x轴交与A，B两点，与y轴交与C点，则能使△ABC是直角三角形的抛物线条数是（ ）
| A、0 | B、1 | C、2 | D、3 |
考点：抛物线与x轴的交点
专题：
分析：首先求出抛物线与坐标轴的交点坐标，然后利用勾股定理求出AB和BC的长，再次根据△ABC是直角三角形，利用勾股定理列出n的一元二次方程，求出n的值即可．
解答：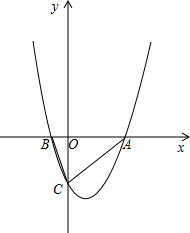
解：令y=（x-n）（x-3）=0，
解得x=n或x=3，
假设3＞n，A（3，0），B（n，0），
令x=0，y=3n，
即C点坐标为（0，3n），
根据图形知：AB2=9+9n2，BC2=n2+9n2，AB2=（3-n）2，
根据题意知△ABC是直角三角形，
即BC2+AC2=AB2，
整理得：9+9n2+n2+9n2=9-6n+n2，
18n2+6n=0，
解得n=0或n=-
，
当n=0时，这样的抛物线不满足题意，
即n=-
，
所以能使△ABC是直角三角形的抛物线条数是1条，
故选B．
解：令y=（x-n）（x-3）=0，解得x=n或x=3，
假设3＞n，A（3，0），B（n，0），
令x=0，y=3n，
即C点坐标为（0，3n），
根据图形知：AB2=9+9n2，BC2=n2+9n2，AB2=（3-n）2，
根据题意知△ABC是直角三角形，
即BC2+AC2=AB2，
整理得：9+9n2+n2+9n2=9-6n+n2，
18n2+6n=0，
解得n=0或n=-
| 1 |
| 3 |
当n=0时，这样的抛物线不满足题意，
即n=-
| 1 |
| 3 |
所以能使△ABC是直角三角形的抛物线条数是1条，
故选B．
点评：本题主要考查了抛物线与x轴的交点的知识点，解答本题的关键是熟练掌握勾股定理的知识，此题是一道比较不错的试题．
练习册系列答案
相关题目
在平面直角坐标系xOy中，以原点O为圆心半径为10的圆，直线y=mx-4m+3与⊙O交于A、B两点，则弦AB的长的最小值为（ ）
A、10
| ||
B、10
| ||
| C、16 | ||
| D、20 |
如图，在平行四边形ABCD中，E为CD上一点，连接AE、BE、BD，且AE、BD交于点F，S△DEF：S△EBF：S△ABF=9：21：49，则DE：EC=（ ）| A、2：3 | B、2：5 |
| C、3：4 | D、3：7 |
关于x对不等式组
的整数解仅有-1，-2，那么适合这个不等式组的整数a，b，满足a+b=-10的概率为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
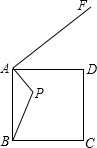已知点P是边长为5的正方形ABCD内一点，且AP=2，AF⊥AP，垂足是点A，若在射线AF上找一点M，使以点A，M，D为顶点的三角形与△ABP相似，则AM为（ ）| A、2 | ||
| B、5 | ||
C、2或
| ||
D、2或
|
下列各运算中，计算正确的是（ ）
| A、3x2+5x2=8x4 | ||||||
B、
| ||||||
C、
| ||||||
D、（-
|
数据1，2，3的方差等于（ ）
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
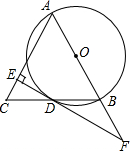如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连结AC，过点D作EF⊥AC，垂足为E，交AB的延长线于点F．