题目内容
7.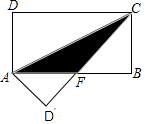 如图,在长方形ABCD中,AB=8,DC=4,将长方形的一角沿AC折叠,则重叠阴影部分△AFC的面积为( )
如图,在长方形ABCD中,AB=8,DC=4,将长方形的一角沿AC折叠,则重叠阴影部分△AFC的面积为( )| A. | 14 | B. | 12 | C. | 10 | D. | 8 |
分析 根据翻折的性质可得∠ACD=∠ACF,根据两直线平行,内错角相等可得∠ACD=∠CAF,从而得到∠ACF=∠CAF,根据等角对等边可得AF=CF,设AF=x,表示出BF、CF,然后利用勾股定理列方程求出x,再根据三角形的面积列式计算即可得解.
解答 解:由翻折得,∠ACD=∠ACF,
∵长方形对边AB∥CD,
∴∠ACD=∠CAF,
∴∠ACF=∠CAF,
∴AF=CF,
设AF=x,则BF=AB-AF=8-x,
CF=AF=x,
在Rt△BCF中,由勾股定理得,BC2+BF2=CF2,
即42+(8-x)2=x2,
解得x=5,
∴重叠阴影部分△AFC的面积=$\frac{1}{2}$AF•BC=$\frac{1}{2}$×5×4=10.
故选C.
点评 本题考查了翻折变换,矩形的性质,勾股定理,翻折前后对应边相等,对应角相等,此类题目,利用勾股定理列出方程是解题的关键,也是难点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.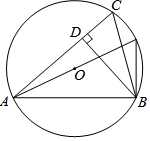 如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则sin∠CBD的值等于( )
如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则sin∠CBD的值等于( )
 如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则sin∠CBD的值等于( )
如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则sin∠CBD的值等于( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
20. 如图,三条直线l1,l2,l3相交于点O,则∠1+∠2+∠3=( )
如图,三条直线l1,l2,l3相交于点O,则∠1+∠2+∠3=( )
 如图,三条直线l1,l2,l3相交于点O,则∠1+∠2+∠3=( )
如图,三条直线l1,l2,l3相交于点O,则∠1+∠2+∠3=( )| A. | 180° | B. | 150° | C. | 120° | D. | 90° |
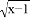 有意义,那么x的取值范围是( )
有意义,那么x的取值范围是( )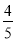 B.
B. 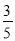 C.
C. 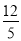 D.
D. 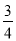
 如图,在Rt△ABC中,∠C=90°,AB=10,点D是直角边AC上一点,且满足cos∠ABD=$\frac{4}{5}$,∠A=∠CBD,求线段BD的长度.
如图,在Rt△ABC中,∠C=90°,AB=10,点D是直角边AC上一点,且满足cos∠ABD=$\frac{4}{5}$,∠A=∠CBD,求线段BD的长度.