题目内容
10. 如图,菱形ABCD中,对角线AC、BD交于点O,点E是BC的中点,若OE=3,则BC的长为( )
如图,菱形ABCD中,对角线AC、BD交于点O,点E是BC的中点,若OE=3,则BC的长为( )| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
分析 利用三角形的中位线定理求出CD,再根据菱形的性质BC=CD即可解决问题.
解答 解: ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴BC=CD,OB=OD,
∵BE=CE,
∴CD=2OE=6,
∴BC=6,
故选B.
点评 本题考查菱形的性质.三角形的中位线定理等知识,解题的关键是熟练掌握三角形的中位线定理解决问题,属于中考常考题型.

练习册系列答案
相关题目
1.随着互联网进入成熟发展阶段,手机已成为我们生活中必不可少的信息交流工具,某商场计划购进A、B两种不同品牌的手机共50部,A、B两种品牌的手机的进价和售价如表所示:
设该商场计划购进A品牌手机x台,两种品牌的手机全部销售完后可获得利润为y元.
(1)求y与x之间的函数关系式;
(2)若商场购进B品牌手机的数量为20部,两种品牌的手机全部销售完后可获利多少?
| 品牌 价格 | A品牌 | B品牌 |
| 进价(元/部) | 3800 | 3000 |
| 售价(元/部) | 4500 | 3500 |
(1)求y与x之间的函数关系式;
(2)若商场购进B品牌手机的数量为20部,两种品牌的手机全部销售完后可获利多少?
18.下列各式属于最简二次根式的是( )
| A. | $\sqrt{0.2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{12}$ |
5. 如图,已知直线a∥b,∠1=50°,则∠2的度数为( )
如图,已知直线a∥b,∠1=50°,则∠2的度数为( )
 如图,已知直线a∥b,∠1=50°,则∠2的度数为( )
如图,已知直线a∥b,∠1=50°,则∠2的度数为( )| A. | 40° | B. | 50° | C. | 130° | D. | 150° |
19.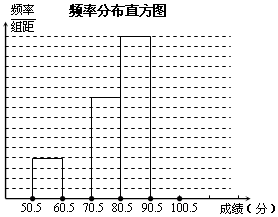 为了让学生了解环保知识,增强环保意识,红星中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,红星中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
(1)填充频率分布表中的空格;
(2)补全频率分布直方图;
(3)在该问题中的样本容量是多少?
答:50.
(4)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?(不要求说明理由)”
答:80.5-90.5.
(5)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
答:216.
 为了让学生了解环保知识,增强环保意识,红星中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,红星中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:| 频率分布表 | ||
| 分组 | 频数 | 频率 |
| 50.5-60.5 | 4 | 0.08 |
| 60.5-70.5 | 8 | 0.16 |
| 70.5-80.5 | 10 | 0.20 |
| 80.5-90.5 | 16 | 0.32 |
| 90.5-100.5 | 12 | 0.24 |
| 合计 | □ | □ |
(2)补全频率分布直方图;
(3)在该问题中的样本容量是多少?
答:50.
(4)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?(不要求说明理由)”
答:80.5-90.5.
(5)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
答:216.
20. 为进一步加强中小学生近视眼的防控工作,某地区教育主管部门对初二年级学生的视力进行了一次抽样调查,经数据分组整理,绘制的频数分布表与频数分布直方图的一部分如下(每组含前一个边界值,不含后一个边界值):
为进一步加强中小学生近视眼的防控工作,某地区教育主管部门对初二年级学生的视力进行了一次抽样调查,经数据分组整理,绘制的频数分布表与频数分布直方图的一部分如下(每组含前一个边界值,不含后一个边界值):
某地区初二学生视力抽样调查频数分布表
请根据以上信息解答下列问题:
(1)表中的a=60,b=0.30;
(2)在图中补全频数分布直方图;
(3)若视力在5.0以上(含5.0)均属正常,根据抽样调查数据,估计该地区6200名初二年级学生视力正常的有3100人.
 为进一步加强中小学生近视眼的防控工作,某地区教育主管部门对初二年级学生的视力进行了一次抽样调查,经数据分组整理,绘制的频数分布表与频数分布直方图的一部分如下(每组含前一个边界值,不含后一个边界值):
为进一步加强中小学生近视眼的防控工作,某地区教育主管部门对初二年级学生的视力进行了一次抽样调查,经数据分组整理,绘制的频数分布表与频数分布直方图的一部分如下(每组含前一个边界值,不含后一个边界值):某地区初二学生视力抽样调查频数分布表
| 分组 | 频数 | 频率 |
| 4.0~4.2 | 10 | 0.02 |
| 4.2~4.4 | 15 | 0.03 |
| 4.4~4.6 | 75 | 0.15 |
| 4.6~4.8 | a | 0.12 |
| 4.8~5.0 | 90 | 0.18 |
| 5.0~5.2 | 150 | b |
| 5.2~5.4 | 100 | 0.20 |
| 合计 | c | 1.00 |
(1)表中的a=60,b=0.30;
(2)在图中补全频数分布直方图;
(3)若视力在5.0以上(含5.0)均属正常,根据抽样调查数据,估计该地区6200名初二年级学生视力正常的有3100人.
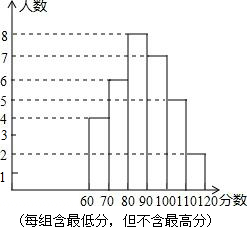 某中学部分同学参加全国初中数学竞赛,取得了优异的成绩,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频数直方图,如图所示.
某中学部分同学参加全国初中数学竞赛,取得了优异的成绩,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频数直方图,如图所示.



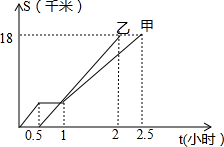 甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离 S(千米)和行驶时间t(小时)之间的关系图象如图2所示,根据图中提供的信息,有下列说法:
甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离 S(千米)和行驶时间t(小时)之间的关系图象如图2所示,根据图中提供的信息,有下列说法: