题目内容
20.观察下面等式:①(a-b)(a+b)=a2-b2;
②(a-b)(a+b)(a2+b2)=(a2-b2)(a2+b2)=(a4-b4);
…
猜想:(x-$\frac{1}{x}$)(x+$\frac{1}{x}$)(x2+$\frac{1}{{x}^{2}}$)(x4+$\frac{1}{{x}^{4}}$)(x8+$\frac{1}{{x}^{8}}$)…(x1024+$\frac{1}{{x}^{1024}}$)=x2048-$\frac{1}{{x}^{2048}}$.
分析 原式结合后,利用平方差公式计算即可得到结果.
解答 解:根据题意得:原式=(x2-$\frac{1}{{x}^{2}}$)(x2+$\frac{1}{{x}^{2}}$)(x4+$\frac{1}{{x}^{4}}$)(x8+$\frac{1}{{x}^{8}}$)…(x1024+$\frac{1}{{x}^{1024}}$)
=(x4-$\frac{1}{{x}^{4}}$)(x4+$\frac{1}{{x}^{4}}$)(x8+$\frac{1}{{x}^{8}}$)…(x1024+$\frac{1}{{x}^{1024}}$)
=…
=x2048-$\frac{1}{{x}^{2048}}$,
故答案为:x2048-$\frac{1}{{x}^{2048}}$
点评 此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目
11.已知一元二次方程x2-6x+8=0的两个根是等腰三角形的底和腰,则这个三角形的周长是( )
| A. | 10 | B. | 8 | C. | 8或10 | D. | 不能确定 |
 一辆货车从百货商店出发,向东走4.5千米到达王颖家,然后向西走1.5千米到达李明家.又向西走8千米达到周斌家,最后回到百货商店.
一辆货车从百货商店出发,向东走4.5千米到达王颖家,然后向西走1.5千米到达李明家.又向西走8千米达到周斌家,最后回到百货商店. 如图,已知AO=DO,CO=BO,求证:△AOC≌△DOB.
如图,已知AO=DO,CO=BO,求证:△AOC≌△DOB.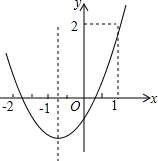 二次函数y=ax2+bx+c的图象如图所示,则下列说法:①abc<0;②2a>b;③a+c>1;④9a+c<3b+2,其中正确的个数是( )
二次函数y=ax2+bx+c的图象如图所示,则下列说法:①abc<0;②2a>b;③a+c>1;④9a+c<3b+2,其中正确的个数是( )