题目内容
已知抛物线y=-x2+6x-5．
（1）通过配方法求抛物线的顶点坐标、对称轴；
（2）当x取何值时，函数有最大值还是最小值？并求出这个最值．
（1）通过配方法求抛物线的顶点坐标、对称轴；
（2）当x取何值时，函数有最大值还是最小值？并求出这个最值．
考点：二次函数的三种形式,二次函数的最值
专题：
分析：（1）利用配方法先提出二次项系数，再加上一次项系数的一半的平方来凑完全平方式，把一般式转化为顶点式，再求出抛物线的顶点坐标、对称轴；
（2）根据二次函数的性质即可求解．
（2）根据二次函数的性质即可求解．
解答：解：（1）∵y=-x2+6x-5=-（x-3）2+4，
∴顶点坐标为（3，4），对称轴为直线x=3；
（2）∵a=-1＜0，
∴函数有最大值，当x=3时，y最大值=4．
∴顶点坐标为（3，4），对称轴为直线x=3；
（2）∵a=-1＜0，
∴函数有最大值，当x=3时，y最大值=4．
点评：本题考查了二次函数的解析式的三种形式：
（1）一般式：y=ax2+bx+c（a≠0，a、b、c为常数）；
（2）顶点式：y=a（x-h）2+k；
（3）交点式（与x轴）：y=a（x-x1）（x-x2）．
同时考查了二次函数的性质．
（1）一般式：y=ax2+bx+c（a≠0，a、b、c为常数）；
（2）顶点式：y=a（x-h）2+k；
（3）交点式（与x轴）：y=a（x-x1）（x-x2）．
同时考查了二次函数的性质．
练习册系列答案
相关题目
下列方程是关于x的一元二次方程的是（ ）
A、
| ||
| B、mx2+mx+5=0 | ||
| C、2x2+3=x（2x-1） | ||
| D、（x+1）2=3x+1 |
实数x、y满足（x2+y2-2）（x2+y2+1）=0，则x2+y2的值为（ ）
| A、2或-1 | B、-2或1 |
| C、2 | D、-1 |
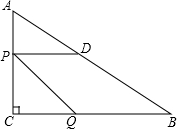如图，在Rt△ABC中，∠C=90°，AC=6，BC=12，动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动，动点Q从点C沿边CB向点B以每秒2个单位长度的速度运动，过点P作PD⊥AC，交AB于点D，连接PQ．点P，Q分别从A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒（t≥0）．
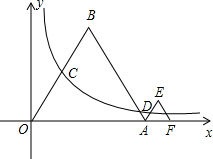如图，等边△OAB和等边△AFE的一边都在x轴上，双曲线y=
如图，在△ABC中，∠ACB=90°，CD⊥AB于点D，E是BC的中点，∠A=55°，求∠DEC的度数．