题目内容
11. 在平面直角坐标系中,直线l:y=x-1与x轴交于点A,如图所示依次作正方形A1B1C1O正方形A2B2C2C1-1,…使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点B1的坐标是(1,1),Bn的坐标是(2n-1,2n-1)(n为正整数).
在平面直角坐标系中,直线l:y=x-1与x轴交于点A,如图所示依次作正方形A1B1C1O正方形A2B2C2C1-1,…使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点B1的坐标是(1,1),Bn的坐标是(2n-1,2n-1)(n为正整数).
分析 根据一次函数图象上点的坐标特征找出A1、A2、A3、A4的坐标,结合图形即可得知点Bn是线段CnAn+1的中点,由此即可得出点Bn的坐标.
解答 解:观察,发现:A1(1,0),A2(2,1),A3(4,3),A4(8,7),…,
∴An(2n-1,2n-1-1)(n为正整数).
观察图形可知:B1(1,1);点Bn是线段CnAn+1的中点,
∴点Bn的坐标是(2n-1,2n-1).
故答案为:(1,1),(2n-1,2n-1)(n为正整数).
点评 本题考查了一次函数图象上点的坐标特征以及规律型中点的坐标的变化,根据点的坐标的变化找出变化规律“An(2n-1,2n-1-1)(n为正整数)”是解题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
6.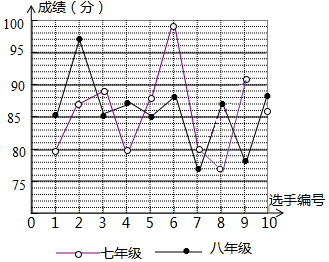 在“创建全国文明城市”演讲比赛中,学校根据初赛成绩在七、八年级分别选出10名同学参加决赛,这些选手的决赛成绩如图所示:
在“创建全国文明城市”演讲比赛中,学校根据初赛成绩在七、八年级分别选出10名同学参加决赛,这些选手的决赛成绩如图所示:
根据如图和表提供的信息,解答下列问题:
(1)请你把上边的表格填写完整;
(2)考虑平均数与方差,你认为八年级的团体成绩更好些;
(3)假设在每个年级的决赛选手中分别选出3人参加总决赛,你认为哪个年级的实力更强一些?请说明理由.
 在“创建全国文明城市”演讲比赛中,学校根据初赛成绩在七、八年级分别选出10名同学参加决赛,这些选手的决赛成绩如图所示:
在“创建全国文明城市”演讲比赛中,学校根据初赛成绩在七、八年级分别选出10名同学参加决赛,这些选手的决赛成绩如图所示:| 团体成绩 | 众数 | 平均数 | 方差 |
| 七年级 | 80 | 85.7 | 39.6 |
| 八年级 | 85 | 85.7 | 27.81 |
(1)请你把上边的表格填写完整;
(2)考虑平均数与方差,你认为八年级的团体成绩更好些;
(3)假设在每个年级的决赛选手中分别选出3人参加总决赛,你认为哪个年级的实力更强一些?请说明理由.

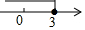
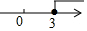
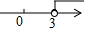
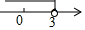
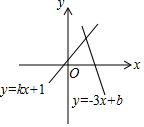 一次函数y=-3x+b和y=kx+1的图象如图所示,其交点为P(3,4),则不等式kx+1≥-3x+b的解集在数轴上表示正确的是( )
一次函数y=-3x+b和y=kx+1的图象如图所示,其交点为P(3,4),则不等式kx+1≥-3x+b的解集在数轴上表示正确的是( )