题目内容
1．
在Rt△ABC中，AC=BC=6，以A为旋转中心将△ABC顺时针旋转30°得到△ADE，则图中阴影部分的面积=3π．
分析 根据勾股定理得到AB=6$\sqrt{2}$，根据旋转的性质得到∠CAD=∠BAE=30°，AD=AC=6，AE=AB=6$\sqrt{2}$，于是得到结论．
解答 解：∵在Rt△ABC中，AC=BC=6，
∴AB=6$\sqrt{2}$，
∵以A为旋转中心将△ABC顺时针旋转30°得到△ADE，
∴∠CAD=∠BAE=30°，AD=AC=6，AE=AB=6$\sqrt{2}$，
∴图中阴影部分的面积=S扇形BAE-S扇形CAD=$\frac{30•π×（6\sqrt{2}）^{2}}{360}$-$\frac{30•π×{6}^{2}}{360}$=3π，
故答案为：3π．
点评 本题考查了旋转的性质，等腰直角三角形的性质，扇形的面积的计算，表示出阴影部分的面积等于两个扇形的面积的差是解题的关键，难点在于求出旋转角的度数．
练习册系列答案
相关题目
12．
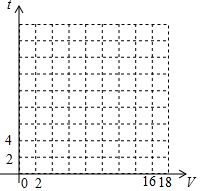某一蓄水池中有水若干吨，若单一个 出水口，排水速度v（m3/h）与排完水池中的水所用的时间之间t（h）的一组对应值如下表：
（1）在如图坐标系中，用描点法画出相应函数的图象；
（2）写出t与v之间的函数关系式；
（3）若5h内排完水池中的水，求排水速度v的范围．
某一蓄水池中有水若干吨，若单一个 出水口，排水速度v（m3/h）与排完水池中的水所用的时间之间t（h）的一组对应值如下表：| 排水速度 （m3/h） | 1 | 2 | 3 | 4 | 6 | 8 | 12 |
| 所用的时间 t（h） | 12 | 6 | 4 | 3 | 2 | 1.5 | 1 |
（2）写出t与v之间的函数关系式；
（3）若5h内排完水池中的水，求排水速度v的范围．
9．
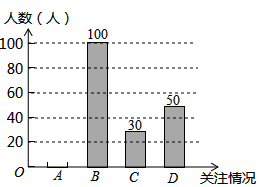温州市政府计划投资百亿元开发瓯江口新区，打造出一个“东方时尚岛、海上新温州”．为了解温州市民对瓯江口新区的关注情况，某学校数学兴趣小组随机采访部分温州市民，对采访情况制作了统计图表的一部分如下：
（1）根据上述统计表可得此次采访的人数为200人；m=20，n=0.15；
（2）根据以上信息补全条形统计图；
（3）根据上述采访结果，估计25000名温州市民中高度关注瓯江口新区的市民约2500人．
温州市政府计划投资百亿元开发瓯江口新区，打造出一个“东方时尚岛、海上新温州”．为了解温州市民对瓯江口新区的关注情况，某学校数学兴趣小组随机采访部分温州市民，对采访情况制作了统计图表的一部分如下：| 关注情况 | 频数 | 频率 |
| A．高度关注 | m | 0.1 |
| B．一般关注 | 100 | 0.5 |
| C．不关注 | 30 | n |
| D．不知道 | 50 | 0.25 |
（2）根据以上信息补全条形统计图；
（3）根据上述采访结果，估计25000名温州市民中高度关注瓯江口新区的市民约2500人．
16．
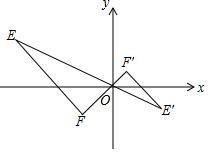如图，已知E′（2，-1），F′（$\frac{1}{2}$，$\frac{1}{2}$），以原点O为位似中心，按比例尺1：2把△EFO扩大，则E′点对应点E的坐标为（ ）
如图，已知E′（2，-1），F′（$\frac{1}{2}$，$\frac{1}{2}$），以原点O为位似中心，按比例尺1：2把△EFO扩大，则E′点对应点E的坐标为（ ）| A． | （-4，2） | B． | （4，-2） | C． | （-1，-1） | D． | （-1，4） |
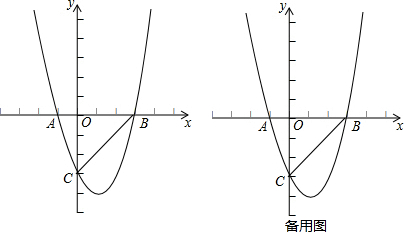
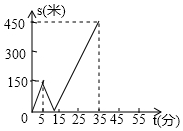甲、乙两人匀速从同一地点到1500m处的图书馆看书，甲出发5min后乙以一定的速度沿同一路线行走．设甲、乙两人相距s（m），甲行走的时间为t（min），s为t的函数，其图象的一部分如图所示．
11．下列运算中，计算正确的是（ ）
| A． | （a2b）3=a5b3 | B． | （3a2）3=27a6 | C． | x6÷x2=x3 | D． | （a+b）2=a2+b2 |