题目内容
15.一个两位数十位上的数字是个位上的数字为2倍,若交换十位与个位上的数字,则所得新两位数与原数的和为99,则这个两位数是63.分析 设原两位数的个位数字为x,十位数字为y,根据等量关系:①十位上的数字是个位上的数字为2倍;②交换十位与个位上的数字,则所得新两位数与原数的和为99;列方程解答即可.
解答 解:设原两位数的个位数字为x,十位数字为y,依题意有
$\left\{\begin{array}{l}{y=2x}\\{10x+y+10y+x=99}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=3}\\{y=6}\end{array}\right.$,
10y+x=60+3=63.
答:这个两位数是63.
故答案为:63.
点评 考查了二元一次方程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.利用二元一次方程组求解的应用题一般情况下题中要给出2个等量关系,准确的找到等量关系并用方程组表示出来是解题的关键.

练习册系列答案
相关题目
6.下列计算正确的是( )
| A. | x3+x3=x6 | B. | x3-x3=x9 | C. | x3÷x-1=x4 | D. | (-x5)(-x)3=-x2 |
 如图,BD是△ABC的角平分线,∠A=40°,∠ABD=35°,求∠C和∠CDB的度数.
如图,BD是△ABC的角平分线,∠A=40°,∠ABD=35°,求∠C和∠CDB的度数.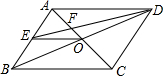 如图,O为?ABCD的对角线交点,E为AB的中点,DE交AC于点F,若S□ABCD=16,则S△DOE的值为2.
如图,O为?ABCD的对角线交点,E为AB的中点,DE交AC于点F,若S□ABCD=16,则S△DOE的值为2.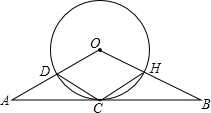 如图,等腰三角形AOB的一边BC经过⊙O上的一点C,AO=BO,CA=CB,OA与⊙O交于点D,OB与⊙O交于点H,连接CD、CH.
如图,等腰三角形AOB的一边BC经过⊙O上的一点C,AO=BO,CA=CB,OA与⊙O交于点D,OB与⊙O交于点H,连接CD、CH.