题目内容
19. 如图,等边△ABC中,AB=2,D为△ABC内一点,且DA=DB,E为△ABC外一点,BE=AB,且∠EBD=∠CBD,连接DE,CE,则下列结论:①∠DAC=∠DBC;②BE⊥AC;③∠DEB=30°;④若EC∥AD,则S△EBC=1,其中正确的有①③④.
如图,等边△ABC中,AB=2,D为△ABC内一点,且DA=DB,E为△ABC外一点,BE=AB,且∠EBD=∠CBD,连接DE,CE,则下列结论:①∠DAC=∠DBC;②BE⊥AC;③∠DEB=30°;④若EC∥AD,则S△EBC=1,其中正确的有①③④.
分析 连接DC,证△ACD≌△BCD得出①∠DAC=∠DBC;再证△BED≌△BCD,得出∠BED=∠BCD=30°;其它两个条件运用假设成立推出答案即可.
解答 证明:连接DC,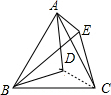
∵△ABC是等边三角形,
∴AB=BC=AC,∠ACB=60,
∵DB=DA,DC=DC,
在△ACD与△BCD中,
$\left\{\begin{array}{l}{AB=BC}\\{DB=DA}\\{DC=DC}\end{array}\right.$,
∴△ACD≌△BCD (SSS),
∴∠BCD=∠ACD=$\frac{1}{2}$∠ACB=30°,
∵BE=AB,
∴BE=BC,
∵∠DBE=∠DBC,BD=BD,
在△BED与△BCD中,
$\left\{\begin{array}{l}{BE=BC}\\{∠DBE=∠DBC}\\{BD=BD}\end{array}\right.$,
∴△BED≌△BCD (SAS),
∴∠BED=∠BCD=30°.
由此得出①③正确.
∵EC∥AD,
∴∠DAC=∠ECA,
∵∠DBE=∠DBC,∠DAC=∠DBC,
∴设∠ECA=∠DBC=∠DBE=∠1,
∵BE=BA,
∴BE=BC,
∴∠BCE=∠BEC=60°+∠1,
在△BCE中三角和为180°,
∴2∠1+2(60°+∠1)=180°
∴∠1=15°,
∴∠CBE=30,这时BE是AC边上的中垂线,结论②才正确.
BE边上的高位$\frac{1}{2}$BC=1,
∴S△EBC=1,结论④是正确的.
故答案为:①③④
点评 本题考查了全等三角形的性质和判定的应用,全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应角相等,对应边相等.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
9. 如图,点B、D、C是⊙O上的点,∠BDC=130°,则∠BOC是( )
如图,点B、D、C是⊙O上的点,∠BDC=130°,则∠BOC是( )
 如图,点B、D、C是⊙O上的点,∠BDC=130°,则∠BOC是( )
如图,点B、D、C是⊙O上的点,∠BDC=130°,则∠BOC是( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
4.下列命题中,假命题是( )
| A. | 两条直角边对应相等的两个直角三角形全等 | |
| B. | 有一个角是60°的等腰三角形是等边三角形 | |
| C. | 顶角相等的两个等腰三角形全等 | |
| D. | 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边分别相等,那么这两个直角三角形全等 |
8.下列说法正确的是( )
| A. | 7是49的算术平方根,即$\sqrt{49}$=±7 | B. | 7是(-7)2的平方根,即$\sqrt{(-7)^{2}}$=7 | ||
| C. | ±7是49的平方根,即±$\sqrt{49}$=7 | D. | ±7是49的平方根,即$\sqrt{49}$=±7 |
 如图,在△ABC中,点D、E分别在AB,AC边上,DE∥BC.若AE:EC=3:1,AD=6,则BD等于( )
如图,在△ABC中,点D、E分别在AB,AC边上,DE∥BC.若AE:EC=3:1,AD=6,则BD等于( ) 如图在Rt△ABC中,∠C=90°,BD平分∠ABC,过D作DE⊥BD交AB于点E,经过B,D,E三点作⊙O.
如图在Rt△ABC中,∠C=90°,BD平分∠ABC,过D作DE⊥BD交AB于点E,经过B,D,E三点作⊙O. 已知,如图,AB∥CD,E是AB的中点,CE=DE,求证:AC=BD.
已知,如图,AB∥CD,E是AB的中点,CE=DE,求证:AC=BD.