题目内容
8. 如图,一只小虫在⊙O内自由爬行(可视为点P),则它进入阴影区域,即正方形AOBC内(C在圆上)的概率为$\frac{1}{2π}$.
如图,一只小虫在⊙O内自由爬行(可视为点P),则它进入阴影区域,即正方形AOBC内(C在圆上)的概率为$\frac{1}{2π}$.
分析 观察图形发现正方形的对角线的长等于圆的半径的长,据此分别表示出正方形的面积和圆的面积,从而求得概率.
解答 解:设⊙O的半径为r,则正方形的半径为r,
则正方形的边长为$\frac{r}{\sqrt{2}}$=$\frac{\sqrt{2}r}{2}$,
所以正方形的面积为$\frac{1}{2}$r2,
因为圆的面积为πr2,
所以它进入阴影区域,即正方形AOBC内(C在圆上)的概率为$\frac{\frac{1}{2}{r}^{2}}{π{r}^{2}}$=$\frac{1}{2π}$,
故答案为:$\frac{1}{2π}$.
点评 本题考查了几何概率,用到的知识点为:概率=相应的面积与总面积之比.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
18.关于反比例函数y=-$\frac{10}{x}$的图象,下列说法错误的是( )
| A. | 在第二,四象限 | B. | 和坐标轴都不相交 | ||
| C. | 绕着原点旋转180°后能与原图重合 | D. | 当x增大时,y一定减小 |
16. 如图,C、D是线段AB上两点,分别以点A和点B为圆心,AD、BC长为半径作弧,两弧相交于点M,连接AM、BM,测量∠AMB的度数,结果为( )
如图,C、D是线段AB上两点,分别以点A和点B为圆心,AD、BC长为半径作弧,两弧相交于点M,连接AM、BM,测量∠AMB的度数,结果为( )
 如图,C、D是线段AB上两点,分别以点A和点B为圆心,AD、BC长为半径作弧,两弧相交于点M,连接AM、BM,测量∠AMB的度数,结果为( )
如图,C、D是线段AB上两点,分别以点A和点B为圆心,AD、BC长为半径作弧,两弧相交于点M,连接AM、BM,测量∠AMB的度数,结果为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
17.同时满足不等式y>-1和y<2的整数有多少个?( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图所示,△ABC内接于⊙O,sinB=$\frac{3}{5}$,AC=2cm,则⊙O的半径为多少厘米?
如图所示,△ABC内接于⊙O,sinB=$\frac{3}{5}$,AC=2cm,则⊙O的半径为多少厘米?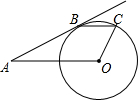 如图,AB切⊙O于点B,OA=5$\sqrt{5}$,tanA=$\frac{1}{2}$,弦BC∥OA
如图,AB切⊙O于点B,OA=5$\sqrt{5}$,tanA=$\frac{1}{2}$,弦BC∥OA