题目内容
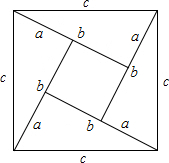利用四个全等的直角三角形可以拼成如图所示的图形，这个图形被称为弦图．观察图形，可以验证公式．
- A.（a+b）（a-b）=a2-b2
- B.（a+b）2=a2-2ab+b2
- C.c2=a2+b2
- D.（a-b）2=a2-2ab+b2
C
分析：利用两种方法表示出大正方形的面积，根据面积相等可以整理出c2=a2+b2．
解答：∵大正方形的面积表示为：c2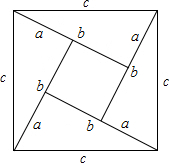
又可以表示为：
ab×4+（b-a）2，
∴c2=ab×4+（b-a）2，
c2=2ab+b2-2ab+a2，
∴c2=a2+b2．
故选：C．
点评：此题考查的知识点是勾股定理得证明，关键是利用三角形和正方形边长的关系进行组合图形，利用面积的关系证明勾股定理．
分析：利用两种方法表示出大正方形的面积，根据面积相等可以整理出c2=a2+b2．
解答：∵大正方形的面积表示为：c2
又可以表示为：
ab×4+（b-a）2，∴c2=
ab×4+（b-a）2，c2=2ab+b2-2ab+a2，
∴c2=a2+b2．
故选：C．
点评：此题考查的知识点是勾股定理得证明，关键是利用三角形和正方形边长的关系进行组合图形，利用面积的关系证明勾股定理．
练习册系列答案
相关题目
利用四个全等的直角三角形可以拼成如图所示的图形，这个图形被称为弦图．观察图形，可以验证（ ）公式．
利用四个全等的直角三角形可以拼成如图所示的图形，这个图形被称为弦图．从图中可以看到：大正方形面积=小正方形面积+四个直角三角形面积．
利用四个全等的直角三角形可以拼成如图所示的图形，这个图形被称为弦图．从图中可以看到：大正方形面积=小正方形面积+四个直角三角形面积．