题目内容
若(a+b)2=5,(a-b)2=2,求a2+b2+ab的值.
考点:完全平方公式
专题:
分析:先根据完全平方公式展开,两式相减即可求出ab,再根据公式求出即可.
解答:解:∵(a+b)2=5,(a-b)2=2,
∴①a2+2ab+b2=5,②a2-2ab+b2=2,
∴①-②得:4ab=3,
∴ab=
,
∴a2+b2+ab=(a+b)2-ab=5-
=4
.
∴①a2+2ab+b2=5,②a2-2ab+b2=2,
∴①-②得:4ab=3,
∴ab=
| 3 |
| 4 |
∴a2+b2+ab=(a+b)2-ab=5-
| 3 |
| 4 |
| 1 |
| 4 |
点评:本题考查了对完全平方公式的应用,注意:(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.

练习册系列答案
相关题目
下列分式中,无论x取什么值,总是有意义的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
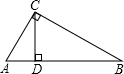 如图,在△ABC中,∠C=90°,CD⊥AB,D为垂足,求证:
如图,在△ABC中,∠C=90°,CD⊥AB,D为垂足,求证: