题目内容
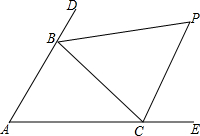 如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:
如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:(1)若∠A=50°,则∠P=
(2)若∠A=90°,则∠P=
(3)若∠A=100°,则∠P=
(4)请你用数学表达式归纳∠A与∠P的关系,并说明理由.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)若∠A=50°,则有∠ABC+∠ACB=130°,∠DBC+∠BCE=360°-130°=230°,根据角平分线的定义可以求得∠PBC+∠PCB的度数,再利用三角形的内角和定理即可求得∠P的度数.
(2)(3)和(1)的解题步骤相似.
(4)利用角平分线的性质和三角形的外角性质可求出∠BCP=
(∠A+∠ABC),∠CBP=
(∠A+∠ACB);再利用三角形内角和定理便可求出∠A与∠P的关系.
(2)(3)和(1)的解题步骤相似.
(4)利用角平分线的性质和三角形的外角性质可求出∠BCP=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵∠A=50°,
∴∠ABC+∠ACB=180°-50°=130°,∠DBC+∠BCE=360°-130°=230°,
又∵∠CBD与∠BCE的平分线相交于点P,
∴∠PBC=
∠DBC,∠PCB=
∠ECB,
∴∠PBC+∠PCB=
(∠DBC+∠ECB)=115°,
∴∠P=65°.
同理得:(2)45°;
(3)40°
(4)∠P=90°-
∠A.理由如下:
∵BP平分∠DBC,CP平分∠BCE,
∴∠DBC=2∠CBP,∠BCE=2∠BCP
又∵∠DBC=∠A+∠ACB∠BCE=∠A+∠ABC,
∴2∠CBP=∠A+∠ACB,2∠BCP=∠A+∠ABC,
∴2∠CBP+2∠BCP=∠A+∠ACB+∠A+∠ABC=180°+∠A,
∴∠CBP+∠BCP=90°+
∠A
又∵∠CBP+∠BCP+∠P=180°,
∴∠P=90°-
∠A.
∴∠ABC+∠ACB=180°-50°=130°,∠DBC+∠BCE=360°-130°=230°,
又∵∠CBD与∠BCE的平分线相交于点P,
∴∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠PBC+∠PCB=
| 1 |
| 2 |
∴∠P=65°.
同理得:(2)45°;
(3)40°
(4)∠P=90°-
| 1 |
| 2 |
∵BP平分∠DBC,CP平分∠BCE,
∴∠DBC=2∠CBP,∠BCE=2∠BCP
又∵∠DBC=∠A+∠ACB∠BCE=∠A+∠ABC,
∴2∠CBP=∠A+∠ACB,2∠BCP=∠A+∠ABC,
∴2∠CBP+2∠BCP=∠A+∠ACB+∠A+∠ABC=180°+∠A,
∴∠CBP+∠BCP=90°+
| 1 |
| 2 |
又∵∠CBP+∠BCP+∠P=180°,
∴∠P=90°-
| 1 |
| 2 |
点评:本题主要考查三角形的一个外角等于和它不相邻的两个内角的和的性质以及角平分线的定义,熟练掌握性质和定义是解题的关键.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
下列说法中正确的是( )
| A、全等三角形是指形状相同的三角形 |
| B、全等三角形的周长和面积分别相等 |
| C、所有的等边三角形是全等三角形 |
| D、有两个角对应相等的两个三角形全等 |
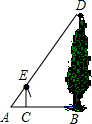 如图,身高为1.6m的某同学想测量一棵大树的高度,她沿树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,求树高.
如图,身高为1.6m的某同学想测量一棵大树的高度,她沿树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,求树高.
 如图,平面直角坐标系的长度单位是厘米,直线y=-
如图,平面直角坐标系的长度单位是厘米,直线y=- 如图,△ABC≌△DEF,点A与D,B与E分别是对应顶点,若测得∠A=∠D=90°,AB=3,DG=1,AG=2,则梯形CFDG的面积是( )
如图,△ABC≌△DEF,点A与D,B与E分别是对应顶点,若测得∠A=∠D=90°,AB=3,DG=1,AG=2,则梯形CFDG的面积是( )