题目内容
解下列方程:
(1)按要求解方程
①
x2+3x-1=0(用配方法)
②x2-2x-4=0(用公式法)
(2)选择合适的方法解方程
③(2y-5)2=4(3y-1)2
④x2-11x+30=0.
(1)按要求解方程
①
| 1 |
| 2 |
②x2-2x-4=0(用公式法)
(2)选择合适的方法解方程
③(2y-5)2=4(3y-1)2
④x2-11x+30=0.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法,解一元二次方程-公式法
专题:计算题
分析:(1)①方程利用配方法求出解即可;②方程利用公式法求出解即可;
(2)①方程开方即可求出解;②方程利用因式分解法求出解即可.
(2)①方程开方即可求出解;②方程利用因式分解法求出解即可.
解答:解:(1)①方程变形得:x2+6x=2,
配方得:x2+6x+9=11,即(x+3)2=11,
开方得:x+3=±
解得:x1=-3+
,x2=-3-
;
②这里a=1,b=-2,c=-4,
∵△=4+16=20,
∴x=
=1±
;
(2)①开方得:2y-5=6y-2或2y-5=2-6y,
解得:y1=-
,y2=
;
②分解因式得:(x-5)(x-6)=0,
解得:x1=5,x2=6.
配方得:x2+6x+9=11,即(x+3)2=11,
开方得:x+3=±
| 11 |
解得:x1=-3+
| 11 |
| 11 |
②这里a=1,b=-2,c=-4,
∵△=4+16=20,
∴x=
2±2
| ||
| 2 |
| 5 |
(2)①开方得:2y-5=6y-2或2y-5=2-6y,
解得:y1=-
| 3 |
| 4 |
| 7 |
| 8 |
②分解因式得:(x-5)(x-6)=0,
解得:x1=5,x2=6.
点评:此题考查了解一元二次方程-因式分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
 如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中错误的是( )
如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中错误的是( )| A、∠COE=∠DOE | ||||
| B、CE=DE | ||||
| C、AE=BE | ||||
D、
|
观察下列图案,既是轴对称图形又是中心对称图形的有( )
A、 |
B、 |
C、 |
D、 |
下列图形中,既是轴对称图形又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |

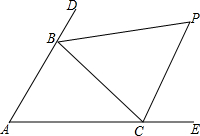 如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:
如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律: