题目内容
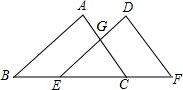 如图,△ABC≌△DEF,点A与D,B与E分别是对应顶点,若测得∠A=∠D=90°,AB=3,DG=1,AG=2,则梯形CFDG的面积是( )
如图,△ABC≌△DEF,点A与D,B与E分别是对应顶点,若测得∠A=∠D=90°,AB=3,DG=1,AG=2,则梯形CFDG的面积是( )| A、5 | B、6 | C、7 | D、8 |
考点:全等三角形的性质
专题:
分析:先求出梯形AGEB的面积等于梯形CFDG的面积,根据全等求出AB=DE=3,求出EG,根据梯形面积公式求出即可.
解答:解:∵△ABC≌△DEF,AB=3,
∴DE=AB=3,
∵DG=1,
∴EG=3-1=2,
∵△ABC≌△DEF,
∴S△ABC=S△DEF,
∴都减去△GEC的面积得:梯形AGEB的面积等于梯形CFDG的面积,
即S梯形CFDG=
(AB+EG)AG=××(3+2)×2=5,
故选A.
∴DE=AB=3,
∵DG=1,
∴EG=3-1=2,
∵△ABC≌△DEF,
∴S△ABC=S△DEF,
∴都减去△GEC的面积得:梯形AGEB的面积等于梯形CFDG的面积,
即S梯形CFDG=
| 1 |
| 2 |
故选A.
点评:本题考查了全等三角形的性质和梯形面积公式的应用,注意:全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
将一元二次方程x2-2x-3=0配方后所得的方程是( )
| A、(x-2)2=4 |
| B、(x-1)2=4 |
| C、(x-1)2=3 |
| D、(x-2)2=3 |
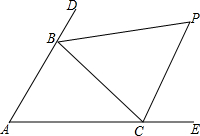 如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:
如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律: 周长为12米的竹篱笆围成一个如图所示的长方形的养鸡场,养鸡场一边靠墙,另三边用竹篱笆围成,如果养鸡场一边长为x米,另一边为y米.
周长为12米的竹篱笆围成一个如图所示的长方形的养鸡场,养鸡场一边靠墙,另三边用竹篱笆围成,如果养鸡场一边长为x米,另一边为y米.