题目内容
 在平面直角坐标系中,Rt△ACB如图放置,∠ACB=90°,∠B=30°,C(0,3),AB=4
在平面直角坐标系中,Rt△ACB如图放置,∠ACB=90°,∠B=30°,C(0,3),AB=4| 3 |
| 3 |
(1)试直接写出A、B两点的坐标.
(2)试判断DE与DC之间的数量关系,并说明理由.
(3)连接AP,在平面直角坐标系中是否存在点Q,使以Q、C、D为顶点的三角形与△ADP全等?若存在,求出点Q的坐标;若不存在,请说明理由.
考点:全等三角形的判定与性质,坐标与图形性质
专题:
分析:(1)易求得tanB的值,即可求得OB的长,即可求得OA的长,即可解题;
(2)根据C,D点坐标可求得CD的长,易求DE的长,即可解题;
(3)点Q位置存在4种情况;分类讨论①∠QCD=120°,QC=AD;②∠QCD=120°,QC=AD;③∠QDC=120°,QD=AD;④∠QDC=120°,QD=AD;即可解题.
(2)根据C,D点坐标可求得CD的长,易求DE的长,即可解题;
(3)点Q位置存在4种情况;分类讨论①∠QCD=120°,QC=AD;②∠QCD=120°,QC=AD;③∠QDC=120°,QD=AD;④∠QDC=120°,QD=AD;即可解题.
解答:解:(1)∵∠B=30°,
∴tanB=
=
,
∴OB=3
,
∵AB=4
,
∴OA=
,
∴点A(-
,0),B(3
,0);
(2)∵C点坐标为(0,3),D点坐标为(
,2),
∴CD=
=2,
∵DE=2,
∴CD=DE;
(3)点Q位置存在4种情况;

∵AE=2
,DE=2,
∴tan∠DAE=30°,AD=4,
∵∠B=30°,
∴∠ADE=∠ADC=60°,
∴∠ADP=120°,
∵△QCD≌△ADP,CD=DP,
∴QC=AD或QD=AD,
①∠QCD=120°,QC=AD=4,
Q点在y轴上,则点Q坐标(0,7);
②∠QCD=120°,QC=AD=4,
∵∠QCD=∠ADB=120°,
∴直线QC斜率为
,
∵直线QC经过点C(0,3),
∴设直线QC解析式为y=
x+3,
∴点Q坐标为(-2
,1);
③∠QDC=120°,QD=AD=4,
Q点在直线x=
上,则点Q坐标(
,-2);
④∠QDC=120°,QD=AD=4,
Q点在直线AD上,
∴点Q坐标(3
,4);
综上所述,点Q坐标为(0,7)或(-2
,1)或(
,-2)或(3
,4).
∴tanB=
| ||
| 3 |
| OC |
| OB |
∴OB=3
| 3 |
∵AB=4
| 3 |
∴OA=
| 3 |
∴点A(-
| 3 |
| 3 |
(2)∵C点坐标为(0,3),D点坐标为(
| 3 |
∴CD=
(
|
∵DE=2,
∴CD=DE;
(3)点Q位置存在4种情况;

∵AE=2
| 3 |
∴tan∠DAE=30°,AD=4,
∵∠B=30°,
∴∠ADE=∠ADC=60°,
∴∠ADP=120°,
∵△QCD≌△ADP,CD=DP,
∴QC=AD或QD=AD,
①∠QCD=120°,QC=AD=4,
Q点在y轴上,则点Q坐标(0,7);
②∠QCD=120°,QC=AD=4,
∵∠QCD=∠ADB=120°,
∴直线QC斜率为
| ||
| 3 |
∵直线QC经过点C(0,3),
∴设直线QC解析式为y=
| ||
| 3 |
∴点Q坐标为(-2
| 3 |
③∠QDC=120°,QD=AD=4,
Q点在直线x=
| 3 |
| 3 |
④∠QDC=120°,QD=AD=4,
Q点在直线AD上,
∴点Q坐标(3
| 3 |
综上所述,点Q坐标为(0,7)或(-2
| 3 |
| 3 |
| 3 |
点评:本题考查了特殊角的三角函数值,考查了三角函数在直角三角形中运用,本题考查了分类讨论思想,本题中根据全等三角形对应边相等性质求解是解题的关键.

练习册系列答案
相关题目
已知12mxn和-
m2n是同类项,则|2-4x|+|4x-1|的值为( )
| 2 |
| 9 |
| A、1 | B、3 | C、8x-3 | D、13 |
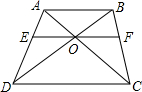 如图所示,在梯形ABCD中,AB∥CD,AB=5,CD=10,AC与BD交于点O,过O作EF∥AB,交AD于E,交BC于F,求EO的长.
如图所示,在梯形ABCD中,AB∥CD,AB=5,CD=10,AC与BD交于点O,过O作EF∥AB,交AD于E,交BC于F,求EO的长. 如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为3,则这个长方形的周长是
如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为3,则这个长方形的周长是 如图,点B为x轴正半轴上一点,点A为双曲线y=
如图,点B为x轴正半轴上一点,点A为双曲线y=