��Ŀ����
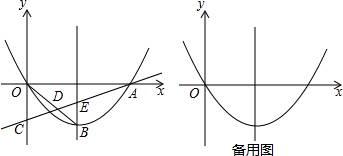
��ƽ��ֱ������ϵxOy�У�������y=mx2-2x��x�������ύ�ڵ�A������ΪB��
��1�����B�����꣨�ú�m�Ĵ���ʽ��ʾ����
��2����֪��C��0��-2����ֱ��AC��BO�ཻ�ڵ�D����������߶Գ��ύ�ڵ�E���ҡ�OCD�ա�BED����m��ֵ��
��3�����ɣ�2��ȷ��������������һ��N��n��-
����N�ڶԳ������࣬��F��G�ڶԳ����ϣ�F��G�Ϸ�����FG=1�����ı���ONGF���ܳ���Сʱ��
�����F�����ꣻ
�����P���������ϣ���y�����Ƿ���ڵ�H��ʹ��N��F��H��PΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����H�����ꣻ�������ڣ���˵�����ɣ�
��1�����B�����꣨�ú�m�Ĵ���ʽ��ʾ����
��2����֪��C��0��-2����ֱ��AC��BO�ཻ�ڵ�D����������߶Գ��ύ�ڵ�E���ҡ�OCD�ա�BED����m��ֵ��
��3�����ɣ�2��ȷ��������������һ��N��n��-
| 5 |
| 3 |
�����F�����ꣻ
�����P���������ϣ���y�����Ƿ���ڵ�H��ʹ��N��F��H��PΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����H�����ꣻ�������ڣ���˵�����ɣ�

���㣺���κ����ۺ���
ר�⣺
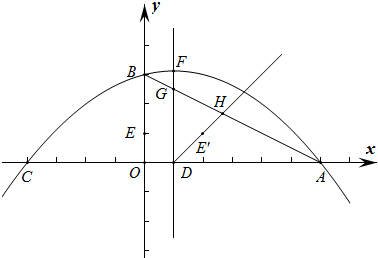
��������1�������䷽����һ��ʽ��Ϊ����ʽ�������������B�����ꣻ
��2���������ߵĶԳ�����x�ύ�ڵ�M������ME��y�ᣬ�ó���AME�ס�AOC���������������ζ�Ӧ�ߵı���ȵó�
=
=
������ME=
OC=1���ٸ��ݡ�OCD�ա�BED���õ�OC=BE=2������BM=BE+ME=3����-
=-3���������m��ֵ��
��3���ɣ�2���������ߵĽ���ʽΪy=
x2-2x����Գ�����x=3��A��6��0����
�ٽ�N��n��-
������y=
x2-2x�����n��ֵ���õ�N�����꣮�����ı���ONGF�У���ON��FGΪ��ֵ�����Ե�NG+OF��Сʱ���ı���ONGF���ܳ���С�����ǿɽ���N����ƽ��1����λ�õ�N�䣨1��-
��������AN�䣬��Գ���Ľ��㼴Ϊ�����F���ڶԳ����Ͻ���F����ƽ��1����λ�õ���G������NG��OF����������֮���߶���̿�֪��ʱ�õ����ı���ONGF���ܳ���С�����ô���ϵ�������ֱ��AN��Ľ���ʽ����x=3���룬���y��ֵ�������õ���F�����ꣻ
 ��N��1��-
��N��1��-
����F��3��-
������H��0��y����������������ۣ�
��NFΪƽ���ı��εı�ʱ��
���NFHPΪƽ���ı��Σ��ɵ�F����ƽ��3����λ������Ϊ0����õ�P�ĺ�����Ϊ1-3=-2����x=-2����y=
x2-2x��
���P�����꣨-2��
������ôN��������ƽ��3����λ��������ƽ��
-��-
��=7����λ����P���������H��������Ϊ-
+7=
�������õ�H������Ϊ��0��
����
���NFPHΪƽ���ı��Σ�ͬ�����H������Ϊ��0��-
����
��NFΪƽ���ı��εĶԽ���ʱ�������NF���е����꣬�ٸ���H��P��������е�����Գƣ����H������Ϊ��0��
����
��2���������ߵĶԳ�����x�ύ�ڵ�M������ME��y�ᣬ�ó���AME�ס�AOC���������������ζ�Ӧ�ߵı���ȵó�
| ME |
| OC |
| AM |
| AO |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| m |
��3���ɣ�2���������ߵĽ���ʽΪy=
| 1 |
| 3 |
�ٽ�N��n��-
| 5 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
 ��N��1��-
��N��1��-| 5 |
| 3 |
| 2 |
| 5 |
��NFΪƽ���ı��εı�ʱ��
���NFHPΪƽ���ı��Σ��ɵ�F����ƽ��3����λ������Ϊ0����õ�P�ĺ�����Ϊ1-3=-2����x=-2����y=
| 1 |
| 3 |
���P�����꣨-2��
| 16 |
| 3 |
| 16 |
| 3 |
| 5 |
| 3 |
| 2 |
| 5 |
| 33 |
| 5 |
| 33 |
| 5 |
���NFPHΪƽ���ı��Σ�ͬ�����H������Ϊ��0��-
| 59 |
| 15 |
��NFΪƽ���ı��εĶԽ���ʱ�������NF���е����꣬�ٸ���H��P��������е�����Գƣ����H������Ϊ��0��
| 3 |
| 5 |
��� �⣺��1����y=mx2-2x=m��x-
�⣺��1����y=mx2-2x=m��x-
��2-
��
�ඥ��B������Ϊ��
��-
����
��2���ߵ�C��0��-2����
��OC=2��
�������ߵĶԳ�����x�ύ�ڵ�M��
��ME��y�ᣬ
���AME�ס�AOC��
��
=
=
��
��ME=
OC=1��
�ߡ�OCD�ա�BED��
��OC=BE=2��
��BM=BE+ME=3��
��-
=-3��
��m=
��
 ��3���ɣ�2���������ߵĽ���ʽΪy=
��3���ɣ�2���������ߵĽ���ʽΪy=
x2-2x����Գ�����ֱ��x=3��A��6��0����
�١ߵ�N��n��-
���ڴ��������ϣ�
��-
=
n2-2n��
���n1=1��n2=5��
�ߵ�N�ڶԳ������࣬
��n=1��
��N��1��-
����
����N����ƽ��1����λ�õ�N�䣨1��-
��������AN�䣬��Գ���Ľ��㼴Ϊ�����F���ڶԳ����Ͻ���F����ƽ��1����λ�õ���G������NG��OF����֪��ʱ�õ����ı���ONGF���ܳ���С����N��F��+AF�䣾AN�䣬�ɵ�NG��+OF�䣾NG+OF����
��ֱ��AN��Ľ���ʽΪy=kx+b��
��N�䣨1��-
����A��6��0�����룬
��
�����
��
��y=
x-
��
�ߵ�F��AN����Գ�����ֱ��x=3�Ľ��㣬
��F��3��-
����
 ��N��1��-
��N��1��-
����F��3��-
������H��0��y����
������������ۣ�
��NFΪƽ���ı��εı�ʱ��FH��NP��FH=NP��
���NFHPΪƽ���ı��Σ�
�ߵ�F����ƽ��3����λ������Ϊ0��
���P�ĺ�����Ϊ1-3=-2��
��x=-2ʱ��y=
x2-2x=
����-2��2-2����-2��=
��
��P��-2��
����
��N��������ƽ��3����λ��������ƽ��
-��-
��=7�������P��
��H��������Ϊ-
+7=
��
��H��������0��
����
���NFPHΪƽ���ı��Σ�
�ߵ�N����ƽ��1����λ������Ϊ0��
���P�ĺ�����Ϊ3-1=2��
��x=2ʱ��y=
x2-2x=
��22-2��2=-
��
��P��2��-
����
��F��������ƽ��1����λ��������ƽ��-
-��-
��=
�������P��
��H��������Ϊ-
-
=-
��
��H��������0��-
����
��NFΪƽ���ı��εĶԽ���ʱ��
��NF���е�����Ϊ��2��-
����
��HP���е�����Ϊ��2��-
����
��H��0��y����
���P�ĺ�����Ϊ4��
��x=4ʱ��y=
x2-2x=
��42-2��4=-
��
��P��4��-
����
��H��������Ϊ2����-
��-��-
��=
��
��H��������0��
����
��������������H��������0��
����0��-
����0��
����
 �⣺��1����y=mx2-2x=m��x-
�⣺��1����y=mx2-2x=m��x-| 1 |
| m |
| 1 |
| m |
�ඥ��B������Ϊ��
| 1 |
| m |
| 1 |
| m |
��2���ߵ�C��0��-2����
��OC=2��
�������ߵĶԳ�����x�ύ�ڵ�M��
��ME��y�ᣬ
���AME�ס�AOC��
��
| ME |
| OC |
| AM |
| AO |
| 1 |
| 2 |
��ME=
| 1 |
| 2 |
�ߡ�OCD�ա�BED��
��OC=BE=2��
��BM=BE+ME=3��
��-
| 1 |
| m |
��m=
| 1 |
| 3 |
 ��3���ɣ�2���������ߵĽ���ʽΪy=
��3���ɣ�2���������ߵĽ���ʽΪy=| 1 |
| 3 |
�١ߵ�N��n��-
| 5 |
| 3 |
��-
| 5 |
| 3 |
| 1 |
| 3 |
���n1=1��n2=5��
�ߵ�N�ڶԳ������࣬
��n=1��
��N��1��-
| 5 |
| 3 |
����N����ƽ��1����λ�õ�N�䣨1��-
| 2 |
| 3 |
��ֱ��AN��Ľ���ʽΪy=kx+b��
��N�䣨1��-
| 2 |
| 3 |
��
|
|
��y=
| 2 |
| 15 |
| 4 |
| 5 |
�ߵ�F��AN����Գ�����ֱ��x=3�Ľ��㣬
��F��3��-
| 2 |
| 5 |
 ��N��1��-
��N��1��-| 5 |
| 3 |
| 2 |
| 5 |
������������ۣ�
��NFΪƽ���ı��εı�ʱ��FH��NP��FH=NP��
���NFHPΪƽ���ı��Σ�
�ߵ�F����ƽ��3����λ������Ϊ0��
���P�ĺ�����Ϊ1-3=-2��
��x=-2ʱ��y=
| 1 |
| 3 |
| 1 |
| 3 |
| 16 |
| 3 |
��P��-2��
| 16 |
| 3 |
��N��������ƽ��3����λ��������ƽ��
| 16 |
| 3 |
| 5 |
| 3 |
��H��������Ϊ-
| 2 |
| 5 |
| 33 |
| 5 |
��H��������0��
| 33 |
| 5 |
���NFPHΪƽ���ı��Σ�
�ߵ�N����ƽ��1����λ������Ϊ0��
���P�ĺ�����Ϊ3-1=2��
��x=2ʱ��y=
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 3 |
��P��2��-
| 8 |
| 3 |
��F��������ƽ��1����λ��������ƽ��-
| 2 |
| 5 |
| 8 |
| 3 |
| 34 |
| 15 |
��H��������Ϊ-
| 5 |
| 3 |
| 34 |
| 15 |
| 59 |
| 15 |
��H��������0��-
| 59 |
| 15 |
��NFΪƽ���ı��εĶԽ���ʱ��
��NF���е�����Ϊ��2��-
| 31 |
| 30 |
��HP���е�����Ϊ��2��-
| 31 |
| 30 |
��H��0��y����
���P�ĺ�����Ϊ4��
��x=4ʱ��y=
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 3 |
��P��4��-
| 8 |
| 3 |
��H��������Ϊ2����-
| 31 |
| 30 |
| 8 |
| 3 |
| 3 |
| 5 |
��H��������0��
| 3 |
| 5 |
��������������H��������0��
| 33 |
| 5 |
| 59 |
| 15 |
| 3 |
| 5 |
�����������Ƕ��κ������ۺ����ͣ������漰�������ߵĶ������������������ε��ж������ʣ�ȫ�������ε����ʣ���ԳƵ����ʣ����ô���ϵ������һ�κ����Ľ���ʽ��ƽ���ı��ε����ʵ�֪ʶ���ۺ��Խ�ǿ����һ���Ѷȣ��������ν�ϡ��������ۼ�����˼���ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
��m������������
+
��ֵ��������
| 1m |
| 2 |
| (-1)m |
| 2 |
| A����0 | B����1��-1 |
| C����-1��0 | D����1��0 |
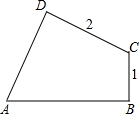 ��ͼ���ı���ABCD�У���DAB=60�㣬��B=��D=90�㣬BC=1��CD=2����Խ���AC�ij���
��ͼ���ı���ABCD�У���DAB=60�㣬��B=��D=90�㣬BC=1��CD=2����Խ���AC�ij��� ��ͼ��ֱ��y=kx-1��x�ᡢy��ֱ���B��C���㣬��
��ͼ��ֱ��y=kx-1��x�ᡢy��ֱ���B��C���㣬��