题目内容
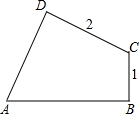如图，四边形ABCD中，∠DAB=60°，∠B=∠D=90°，BC=1，CD=2，求对角线AC的长．考点：勾股定理,含30度角的直角三角形
专题：
分析：延长DC与AB交于一点K．解直角三角形求出DK，再求出AD，利用勾股定理求出AC即可．
解答：
解：延长DC交AB的延长线于点K；
在Rt△ADK中，
∵∠DAK=60°∠AKD=30°，BC=1，
∴CK=2，BK=
，
∴DK=CD+CK=4，
∴AD=
=
，
在△Rt△ADC中，
AC=
=
．
解：延长DC交AB的延长线于点K；在Rt△ADK中，
∵∠DAK=60°∠AKD=30°，BC=1，
∴CK=2，BK=
| 3 |
∴DK=CD+CK=4，
∴AD=
| DK |
| tan60° |
4
| ||
| 3 |
在△Rt△ADC中，
AC=
| AD2+CD2 |
2
| ||
| 3 |
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
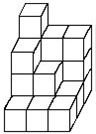把19个棱长为1厘米的正方体重叠在一起，按右图中的方式拼成一个立体图形．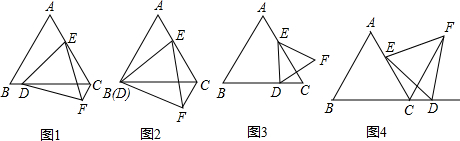
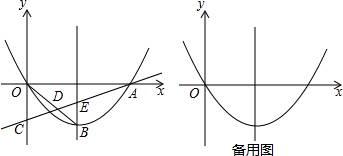
已知实数a、b在数轴上的位置如图所示：试化简：