题目内容
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A(6,0),C(-4,0)两点,与y轴交于点B(0,3).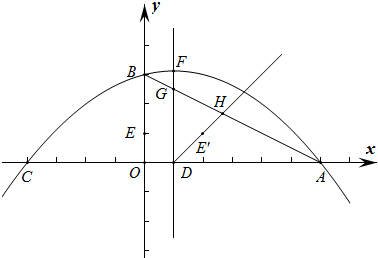
(1)求抛物线的解析式;
(2)点D、点E同时从点O出发以每秒1个单位长度的速度分别沿x轴正半轴,y轴正半轴向点A、点B方向移动,当点D运动到点A时,点D、E同时停止移动.过点D作x轴的垂线交抛物线于点F,交AB于点G,作点E关于直线DF的对称点E′,连接FE′,射线DE′交AB于点H.设运动时间为t秒.
①t为何值时点E′恰好在抛物线上,并求此时△DE′F与△ADG重叠部分的面积;
②点P是平面内任意一点,若点D在运动过程中的某一时刻,形成以点A、E′、D、P为顶点的四边形是菱形,那么请直接写出点P的坐标.

(1)求抛物线的解析式;
(2)点D、点E同时从点O出发以每秒1个单位长度的速度分别沿x轴正半轴,y轴正半轴向点A、点B方向移动,当点D运动到点A时,点D、E同时停止移动.过点D作x轴的垂线交抛物线于点F,交AB于点G,作点E关于直线DF的对称点E′,连接FE′,射线DE′交AB于点H.设运动时间为t秒.
①t为何值时点E′恰好在抛物线上,并求此时△DE′F与△ADG重叠部分的面积;
②点P是平面内任意一点,若点D在运动过程中的某一时刻,形成以点A、E′、D、P为顶点的四边形是菱形,那么请直接写出点P的坐标.
考点:二次函数综合题
专题:
分析:(1)根据待定系数法即可求得解析式;
(2)①根据题意设E′(2t,t),代入抛物线的解析式即可求得t的值,进而求得D、E′的坐标,根据A(6,0),B(0,3)求得直线AB的解析式,根据D(2,0),E′(4,2)求得直线DE′的解析式,进而求得G、H的坐标,即可求得三角形DGH的面积,即是△DE′F与△ADG重叠部分的面积;
②根据菱形的性质分三种情况分别讨论即可求得P的坐标;
(2)①根据题意设E′(2t,t),代入抛物线的解析式即可求得t的值,进而求得D、E′的坐标,根据A(6,0),B(0,3)求得直线AB的解析式,根据D(2,0),E′(4,2)求得直线DE′的解析式,进而求得G、H的坐标,即可求得三角形DGH的面积,即是△DE′F与△ADG重叠部分的面积;
②根据菱形的性质分三种情况分别讨论即可求得P的坐标;
解答:解:(1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于A(6,0),C(-4,0)两点,与y轴交于点B(0,3).
∴
,解得
,
∴抛物线的解析式为y=-
x2+
x+3;
(2)①根据题意设E′(2t,t),
∴t=-
×4t2+
×t+3,解得:t=2,t=-3(舍去),
∴D(2,O),E′(4,2)
∵A(6,0),B(0,3).
∴直线AB为y=-
x+3,
把x=2代入得y=-
×2+3=2,
∴G(2,2),
∵D(2,0),E′(4,2),
∴直线DE′的解析式为y=x-2,
解
,得
,
∴H(
,
),
∴S△DGH=
×2×(
-2)=
,
∴t为2时点E′恰好在抛物线上,此时△DE′F与△ADG重叠部分的面积为
;
②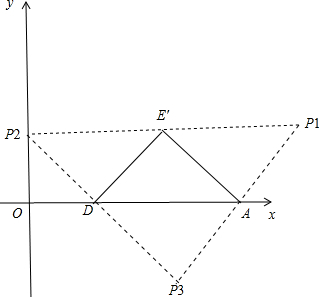 如图,当AD为对角线时,∵A(6,0),D(2,0),E′(4,2),以点A、E′、D、P为顶点的四边形是菱形,
如图,当AD为对角线时,∵A(6,0),D(2,0),E′(4,2),以点A、E′、D、P为顶点的四边形是菱形,
则DE′=AE′,
∴E′和P关于x轴对称,
∴P(4,-2)
所以点P的坐标为(4,-2);
当AD、DE是边时;∵AD=6-t,菱形ADE′P
∴E'P=AD=DE′=6-t
∵E'(2t,t),D(t,0)
∴DE′2=t2+t2=2t2
∴2t2=(6-t)2
∴t1=-6+6
,t2=-6-6
(舍去),
∵P(t+6,t)
∴P(6
,-6+6
),
当AD、AE是边时;∵AD=6-t,菱形AE'PD
∴E'P=AD=AE′=6-t,
∵E'(2t,t),D(t,0),
∵AE′2=(6-2t)2+t2,
∴(6-2t)2+t2=(6-t)2,
∴t3=3,t4=0(舍去),
∴P(3,3).
综上,P(4,-2)或P(6
,-6+6
)或(3,3).
∴
|
|
∴抛物线的解析式为y=-
| 1 |
| 8 |
| 1 |
| 4 |
(2)①根据题意设E′(2t,t),
∴t=-
| 1 |
| 8 |
| 1 |
| 4 |
∴D(2,O),E′(4,2)
∵A(6,0),B(0,3).
∴直线AB为y=-
| 1 |
| 2 |
把x=2代入得y=-
| 1 |
| 2 |
∴G(2,2),
∵D(2,0),E′(4,2),
∴直线DE′的解析式为y=x-2,
解
|
|
∴H(
| 10 |
| 3 |
| 4 |
| 3 |
∴S△DGH=
| 1 |
| 2 |
| 10 |
| 3 |
| 4 |
| 3 |
∴t为2时点E′恰好在抛物线上,此时△DE′F与△ADG重叠部分的面积为
| 4 |
| 3 |
②
 如图,当AD为对角线时,∵A(6,0),D(2,0),E′(4,2),以点A、E′、D、P为顶点的四边形是菱形,
如图,当AD为对角线时,∵A(6,0),D(2,0),E′(4,2),以点A、E′、D、P为顶点的四边形是菱形,则DE′=AE′,
∴E′和P关于x轴对称,
∴P(4,-2)
所以点P的坐标为(4,-2);
当AD、DE是边时;∵AD=6-t,菱形ADE′P
∴E'P=AD=DE′=6-t
∵E'(2t,t),D(t,0)
∴DE′2=t2+t2=2t2
∴2t2=(6-t)2
∴t1=-6+6
| 2 |
| 2 |
∵P(t+6,t)
∴P(6
| 2 |
| 2 |
当AD、AE是边时;∵AD=6-t,菱形AE'PD
∴E'P=AD=AE′=6-t,
∵E'(2t,t),D(t,0),
∵AE′2=(6-2t)2+t2,
∴(6-2t)2+t2=(6-t)2,
∴t3=3,t4=0(舍去),
∴P(3,3).
综上,P(4,-2)或P(6
| 2 |
| 2 |
点评:本题考查了待定系数法求解析式,直线的交点坐标,三角形的面积,以及菱形的性质等,本题的关键是确定D的坐标.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
计算(-
)2006+(-
)2007的结果为( )
| 1 |
| 2 |
| 1 |
| 2 |
A、(-
| ||
B、-(-
| ||
C、
| ||
D、-
|
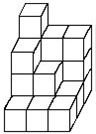 把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.
把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.