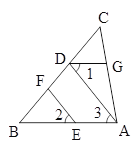题目内容
先化简，再求值：(a＋1－
)÷(
)，其中a＝2＋
.
【答案】3+2
【解析】分析：用分式的混合运算法则把原分式化简，再把a的值代入求解.
详【解析】
(a＋1－
)÷(
)
＝(
－)÷(
)
＝
·
＝a(a－2).
当a＝2＋时，
原式＝(2＋)(2＋－2)
＝3＋
.
点睛：对于分式化简求值问题，要先确定运算顺序，再根据分式的混合运算法则进行计算，最后把相关字母的值代入化简后的式子求值．当分子分母是多项式时，应先分解因式，如果分子分母有公因式，要约分．
【题型】解答题
【结束】
20
已知：如图，在△ABC中，AB=AC，AD是BC边上的中线，AE∥BC，CE⊥AE，垂足为E．
（1）求证：△ABD≌△CAE；
（2）连接DE，线段DE与AB之间有怎样的位置和数量关系？请证明你的结论．
练习册系列答案
相关题目
某书店为了迎接“读书节”制定了活动计划，以下是活动计划书的部分信息：
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位：元) | 18 | 12 |
备注 | 1.用不超过16800元购进A，B两类图书共1000本； 2．A类图书不少于600本； …… |
(1)陈经理查看计划数时发现：A类图书的标价是B类图书标价的1.5倍，若顾客用540元购买图书，能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本，请求出A，B两类图书的标价；
(2)经市场调查后，陈经理发现他们高估了“读书节”对图书销售的影响，便调整了销售方案，A类图书每本标价降低a元(0＜a＜5)销售，B类图书价格不变，那么书店应如何进货才能获得最大利润？
=1.1， 
=1.2， 
=1.3， 
=1.4）
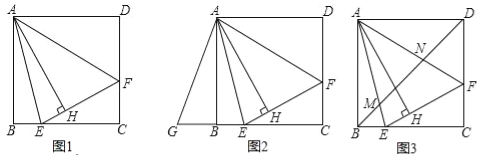
≈1.41，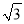 
≈1.73）
π－1 C. π－2 D. 
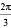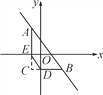
－2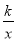
的图象有两个交点A(－1，m)和B，过点A作AE⊥x轴，垂足为E；过点B作BD⊥y轴，垂足为点D，且点D的坐标为(0，－2)，连结DE.
