题目内容
如图,在一笔直的海岸线上有A、B两个观测站,A在B的正东方向,AB=2(单位km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.
(1)求点P到海岸线的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.(上述两小题的结果都保留根号)
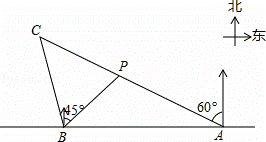
解:(1)如图,过点P作PD⊥AB于点D.设PD=xkm.
在Rt△PBD中,∠BDP=90°,∠PBD=90°﹣45°=45°,
∴BD=PD=xkm.
在Rt△PAD中,∠ADP=90°,∠PAD=90°﹣60°=30°,
 ∴AD=
∴AD=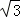 PD=
PD=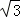 xkm.
xkm.
∵BD+AD=AB,
∴x+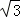 x=2,x=
x=2,x=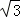 ﹣1,
﹣1,
∴点P到海岸线l的距离为(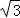 ﹣1)km;
﹣1)km;
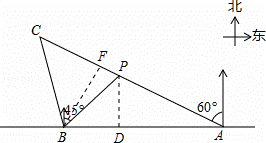
(2)如图,过点B作BF⊥AC于点F.
在Rt△ABF中,∠AFB=90°,∠BAF=30°,
∴BF=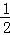 AB=1km.
AB=1km.
在△ABC中,∠C=180°﹣∠BAC﹣∠ABC=45°.
在Rt△BCF中,∠BFC=90°,∠C=45°,
∴BC=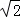 BF=
BF=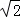 km,…
km,…
∴点C与点B之间的距离为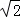 km.
km.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
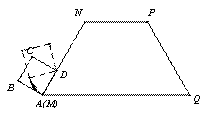
如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正
方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重
合.现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚,
翻滚到有一个顶点与Q重合即停止滚动,求正方形在整个翻滚过程中
| |
面积S=( )
A.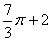 B.
B.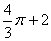 C.
C.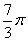 D.
D.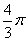
 满足:
满足: ,则代数式
,则代数式 的值是 .
的值是 . ,弦CD=DE=4,连结OB,OD, 则图中两个阴影部分的面积和为( )
,弦CD=DE=4,连结OB,OD, 则图中两个阴影部分的面积和为( )

 的两根是三角形的边,则三角形的第三条边长可以是( )
的两根是三角形的边,则三角形的第三条边长可以是( )
 轴上方作一个正方形D1E1F1G1,
轴上方作一个正方形D1E1F1G1,  ,然后在
,然后在