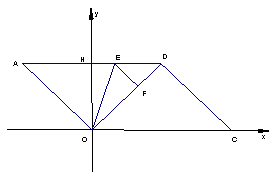
题目内容
点A(-1,0)B(4,0)C(0,2)是平面直角坐标系上的三点。
① 如图10-1先过A、B、C作△ABC,然后在在 轴上方作一个正方形D1E1F1G1,
轴上方作一个正方形D1E1F1G1,
使D1E1在AB上, F1、G1分别在BC、AC上
② 如图10-2先过A、B、C作圆⊙M,然后在 轴上方作一个正方形D2E2F2G2,
轴上方作一个正方形D2E2F2G2,
使D2E2在 轴上 ,F2、G2在圆上
轴上 ,F2、G2在圆上
③ 如图10-3先过A、B、C作抛物线 ,然后在
,然后在 轴上方作一个正方形D3E3F3G3,
轴上方作一个正方形D3E3F3G3,
使D3E3在 轴上, F3、G3在抛物线上
轴上, F3、G3在抛物线上
(1)请比较 正方形D1E1F1G1 , 正方形D2E2F2G2 , 正方形D3E3F3G3 的面积大小
(2)并简要小结解决此题所用的方法或定理。

解:(1)图10-1 设正方形的边长为
由△CG1F1∽△CAB 得 
∴ ∴
∴
图10-2 设正方形的边长为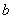
∵A(-1,0)B(4,0)C(0,2)
∴
∴∠ACB=90° ∴AB是圆M的直径
过M作MN⊥G2F2 由垂径定理得
解得 即
即
图10-3 设正方形的边长为
由A(-1,0)B(4,0)C(0,2)得抛物线为
由轴对称性可知 F3( ,
, ) 代入得
) 代入得
解得 ∴
∴
∵
∴ <
< <
<
(2)主要定理有:相似三角形的性质(相似比等于对应高之比),
勾股定理;抛物线的对称性等。

练习册系列答案
相关题目
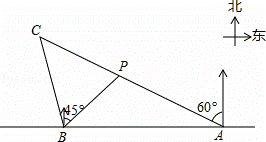
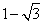 ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P/(1,3)处.过点P/作x轴的平行线交抛物线于C、D两点,则翻折后的图案的高与宽的比为__________(结果可保留根号).
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P/(1,3)处.过点P/作x轴的平行线交抛物线于C、D两点,则翻折后的图案的高与宽的比为__________(结果可保留根号).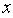 为何实数时,该代数式值恒为正数,并简要说明该代数式值恒为正数的理由。
为何实数时,该代数式值恒为正数,并简要说明该代数式值恒为正数的理由。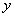 的代数式,并且使代数式有意义的
的代数式,并且使代数式有意义的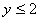 且
且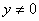 。请你写出的代数式。
。请你写出的代数式。
 的根, 当两圆相内切时,⊙O1与⊙O2的圆心距为( )
的根, 当两圆相内切时,⊙O1与⊙O2的圆心距为( )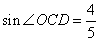 。点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),
。点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),