题目内容
在平面直角坐标系xOy中，抛物线y=mx2﹣2mx﹣2（m≠0）与y轴交于点A，其对称轴与x轴交于点B．
（1）求点A，B的坐标；
（3）若该抛物线在2＜x＜3这一段位于直线AB的下方，
并且在3＜x＜4这一段位于直线AB的上方，求该抛物线的解析式．
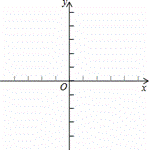
解：（1）当x=0时，y=﹣2，
∴A（0，﹣2），
抛物线的对称轴为直线x=﹣
=1，
∴B（1，0）；
（2）直线AB的解析式为y=2x-2，结合图象可以观察到抛物线在2＜x＜3这一段位于直线AB的下方，在3＜x＜4这一段位于直线AB的上方，
∴抛物线与直线AB的交点的横坐标为3，
当x=3时，y=﹣2×3-2=4，
所以，抛物线过点（3，4），
当x=3时，9m-6m﹣2=4，
解得m=2，
∴抛物线的解析式为y=2x2﹣4x﹣2．
练习册系列答案
相关题目
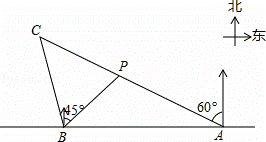
，OP=1，求BC的长．
，则tan B的值为__________．【原创】
图象上三点，作直线l，
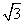）,（1,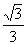
n）(m、n为非负数),则CE+DE+DB的最小值是 ．
B．
C．
D．
(2≤n≤9，n为整数)，则当
,
表示的数互为相反数，那么图中的4个点中，哪一个点表示的数的绝对值最大（ ）
B. 
D.
