题目内容
20.计算:①(-9)-(-7)+(-6)-(+4)-(-5);
②-14$\frac{2}{3}$+11$\frac{2}{15}$-(-12$\frac{2}{3}$)-14+(-11$\frac{2}{15}$);
③4$\frac{3}{4}$-(+3.85)-(-3$\frac{1}{4}$)+(-3.15);
④-0.21+(-5.34)-(+0.15)+|-10$\frac{1}{5}$|.
分析 根据有理数的加减混合运算法则计算即可.
解答 解:①(-9)-(-7)+(-6)-(+4)-(-5)
=-9-6-4+7+5
=-19+12
=-7;
②-14$\frac{2}{3}$+11$\frac{2}{15}$-(-12$\frac{2}{3}$)-14+(-11$\frac{2}{15}$)
=-14$\frac{2}{3}$+12$\frac{2}{3}$-14+(11$\frac{2}{5}$-11$\frac{2}{15}$)
=-16;
③4$\frac{3}{4}$-(+3.85)-(-3$\frac{1}{4}$)+(-3.15)
=4$\frac{3}{4}$+3$\frac{1}{4}$+(-3.85-3.15)
=8-7
=1;
④-0.21+(-5.34)-(+0.15)+|-10$\frac{1}{5}$|
=-0.21-5.34-0.15+10.2
=4.5.
点评 本题考查的是有理数的加减混合运算,掌握有理数的加减混合运算法则是解题的关键.

练习册系列答案
相关题目
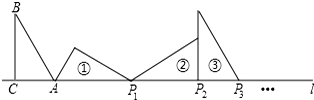
10.如图:在△ABC中,∠ACB=90°,∠B=30°,AC=1,AC在直线l上,将△ABC绕点A顺时针旋转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,可得到点P3,此时AP3=3+$\sqrt{3}$;…,按此规律继续旋转,直到得到点P2015为止,则AP2015=( )

| A. | 2015+672$\sqrt{3}$ | B. | 2013+671$\sqrt{3}$ | C. | 2013+672$\sqrt{3}$ | D. | 2015+671$\sqrt{3}$ |