Question

10．在半径为R的圆中有一条长度为R的弦，则该弦所对的圆周角的度数是30°或150°．

Answer 1

分析 根据题意画出相应的图形，如图所示，由半径等于弦长，得到三角形AOB为等边三角形，利用等边三角形的性质得到∠AOB为60°，利用同弧所对的圆心角等于所对圆周角的2倍求出∠ACB的度数，再利用圆内接四边形的对角1互补求出∠ADB的度数，即可得出弦AB所对圆周角的度数．

解答 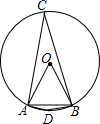解：根据题意画出相应的图形，如图所示，
∵OA=OB=AB，
∴△AOB为等边三角形，
∴∠AOB=60°，
∵∠AOB与∠ACB都对$\widehat{AB}$，
∴∠ACB=$\frac{1}{2}$∠AOB=30°，
又∵四边形ACBD为圆O的内接四边形，
∴∠ACB+∠ADB=180°，
∴∠ADB=150°，
∴弦AB所对的圆周角为30°或150°．
故答案为：30°或150°

点评 此题考查了圆周角定理，等边三角形的性质，以及圆内接四边形的性质，熟练掌握圆周角定理是解本题的关键．