题目内容
14．把下列各式分解因式（1）3x-12x3
（2）-a2-49b2+14ab
（3）x2（x-y）+y2（y-x）
（4）m2n2-18mn+65
（5）9（a-b）2-30（a2-b2）+25（a+b）2．
分析 （1）根据提公因式法，可得平方差公式，根据平方差公式，可得答案；
（2）根据提公因式法，可得完全平方公式，根据完全平方公式，可得答案；
（3）根据提公因式法，可得平方差公式，根据平方差公式，可得答案；
（4）根据十字相乘法，可得答案；
（5）根据完全平方公式，可得答案．
解答 解：（1）原式=3x（1-4x2）=3x（1+2x）（1-2x）；
（2）原式=-（a2+-14ab+49b2）=-（a-7b）2；
（3）原式=（x-y）（x2-y2）=（x-y）（x+y）（x-y）=（x-y）2（x+y）；
（4）原式=（mn-3）（mn-15）；
（5）原式=[3（a-b）-5（a+b）]2=（2a+8b）2．
点评 本题考查了因式分解，一提，二套，三检查，分解要彻底．
练习册系列答案
相关题目
3．菱形和矩形都具有的性质是（ ）
| A． | 对角线互相垂直 | B． | 对角线相等 | C． | 对角线互相平分 | D． | 对角线平分对角 |
5．图1是一个八角星形纸板，图中有八个直角、八个相等的钝角，每条边都相等，如图2将纸板沿虚线进行切割，无缝隙无重叠的拼成如图3所示的大正方形，其面积为8+4$\sqrt{2}$，则图3中线段AB的长为（ ）
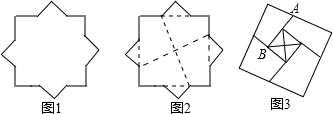
| A． | $\sqrt{2}$ | B． | 2$\sqrt{2}$ | C． | $\sqrt{2}$-1 | D． | $\sqrt{2}$+1 |
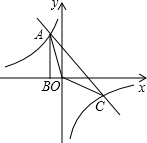如图，Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-（k+1）在第二象限的交点．AB⊥x轴于B，且S△ABO=$\frac{3}{2}$．