题目内容
11.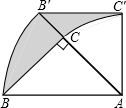 如图,在△ABC中,∠ACB=90°,BC=AC=2,以点A为旋转中心,把△ABC按顺时针方向旋转45°后得到△AB′C′,BC边在上述旋转过程中所扫过部分(阴影部分)的面积是$\frac{1}{2}$π(结果保留π).
如图,在△ABC中,∠ACB=90°,BC=AC=2,以点A为旋转中心,把△ABC按顺时针方向旋转45°后得到△AB′C′,BC边在上述旋转过程中所扫过部分(阴影部分)的面积是$\frac{1}{2}$π(结果保留π).
分析 根据旋转变换只改变图形的位置不改变图形的形状与大小可得△AB′C′和△ABC全等,然后推出阴影部分的面积等于扇形ABB′的面积减去扇形ACC′的面积,再根据扇形的面积公式列式进行计算即可得解.
解答 解:∵在△ABC中,∠ACB=90°,BC=AC=2,
∴AB=2$\sqrt{2}$.
∵△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,
∴△AB′C′≌△ABC,
∴S阴影=S扇形ABB′+S△AB′C′-S△ABC-S扇形ACC′=S扇形ABB′-S扇形ACC′,
∴阴影部分的面积=$\frac{45•π•(2\sqrt{2})^{2}}{360}$-$\frac{45•π×{2}^{2}}{360}$=$\frac{1}{2}$π.
故答案是:$\frac{1}{2}$π.
点评 本题考查了旋转的性质,等腰直角三角形的性质,扇形的面积计算,根据旋转的性质得到两三角形全等,然后推出阴影部分的面积等于两个扇形的面积的差是解题的关键.

练习册系列答案
相关题目
2.在某校初三年级古诗词比赛中,初三(1)班42名学生的成绩统计如下,则该班学生成绩的中位数和众数分别是( )
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数 | 1 | 2 | 8 | 13 | 14 | 4 |
| A. | 70,80 | B. | 70,90 | C. | 80,90 | D. | 90,100 |
16.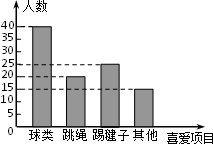 某学校为了解学生大课间体育活动情况,随机抽取本校部分学生进行调查.整理收集到的数据,绘制成如图所示的统计图.小明随机调查一名学生,他喜欢“踢毽子”的概率是( )
某学校为了解学生大课间体育活动情况,随机抽取本校部分学生进行调查.整理收集到的数据,绘制成如图所示的统计图.小明随机调查一名学生,他喜欢“踢毽子”的概率是( )
 某学校为了解学生大课间体育活动情况,随机抽取本校部分学生进行调查.整理收集到的数据,绘制成如图所示的统计图.小明随机调查一名学生,他喜欢“踢毽子”的概率是( )
某学校为了解学生大课间体育活动情况,随机抽取本校部分学生进行调查.整理收集到的数据,绘制成如图所示的统计图.小明随机调查一名学生,他喜欢“踢毽子”的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{20}$ |
3.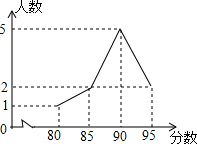 在一次演讲比赛中,参赛的10名学生成绩统计如图所示,下列说法中错误的是( )
在一次演讲比赛中,参赛的10名学生成绩统计如图所示,下列说法中错误的是( )
 在一次演讲比赛中,参赛的10名学生成绩统计如图所示,下列说法中错误的是( )
在一次演讲比赛中,参赛的10名学生成绩统计如图所示,下列说法中错误的是( )| A. | 众数是90分 | B. | 中位数是90分 | C. | 平均数是90分 | D. | 极差是15分 |
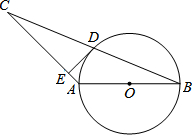 如图,△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作⊙O的切线DE交AC于点E.
如图,△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,过点D作⊙O的切线DE交AC于点E.
 在平面直角坐标系xOy中,抛物线y=$\frac{1}{2}{x^2}$-x+2与y轴交于点A,顶点为点B,点C与点A关于抛物线的对称轴对称.
在平面直角坐标系xOy中,抛物线y=$\frac{1}{2}{x^2}$-x+2与y轴交于点A,顶点为点B,点C与点A关于抛物线的对称轴对称.