题目内容
1.如图所示,根据变化规律填空:
(1)第10个图中有55个三角形;
(2)第n个图中有$\frac{n(n+1)}{2}$个三角形.
分析 根据已知图形编号与三角形个数的关系,然后总结归纳其中的规律,写出其通项,将n=10代入可得答案.
解答 解:第1个图中,共有1个三角形;
第2个图中,共有1+2=3个三角形;
第3个图中,共有1+2+3=6个三角形;
第4个图中,共有1+2+3+4=10个三角形;
第5个图中,共有1+2+3+4+5=15个三角形;
…
由此归纳可得:
第n个图中,共有1+2+3+4+…+n=$\frac{n(n+1)}{2}$个三角形;
当n=10时,$\frac{10×11}{2}$=55,
故第10个图中三角形的个数是55个,
第n个图中三角形的个数是$\frac{n(n+1)}{2}$个;
故答案为:(1)55;(2)$\frac{n(n+1)}{2}$.
点评 本题考查的知识点是归纳推理,归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
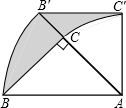 如图,在△ABC中,∠ACB=90°,BC=AC=2,以点A为旋转中心,把△ABC按顺时针方向旋转45°后得到△AB′C′,BC边在上述旋转过程中所扫过部分(阴影部分)的面积是$\frac{1}{2}$π(结果保留π).
如图,在△ABC中,∠ACB=90°,BC=AC=2,以点A为旋转中心,把△ABC按顺时针方向旋转45°后得到△AB′C′,BC边在上述旋转过程中所扫过部分(阴影部分)的面积是$\frac{1}{2}$π(结果保留π).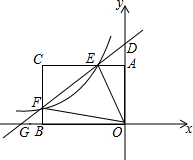 如图,矩形AOBC的顶点坐标分别为A(0,3),O(0,0),B(-4,0),C(-4,3)动点F在BC上(不与B、C重合)过点F的反比例函数y=$\frac{k}{x}$的图象与边AB交于点E,直线EF分别与y轴和x轴相交于点D,G
如图,矩形AOBC的顶点坐标分别为A(0,3),O(0,0),B(-4,0),C(-4,3)动点F在BC上(不与B、C重合)过点F的反比例函数y=$\frac{k}{x}$的图象与边AB交于点E,直线EF分别与y轴和x轴相交于点D,G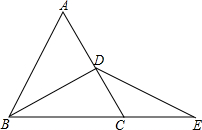 已知:如图,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使CE=CD,试说明:∠DBC=∠E.
已知:如图,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使CE=CD,试说明:∠DBC=∠E.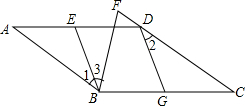 已知平行四边形ABCD中,G为BC中点,点E在AD边上,且∠1=∠2.
已知平行四边形ABCD中,G为BC中点,点E在AD边上,且∠1=∠2.