题目内容
6. 如图,在△ABC中,D是BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF,求证:
如图,在△ABC中,D是BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF,求证:(1)BE=CF;
(2)AB=AC.
分析 (1)运用HL定理证明△BDE≌△CDF,进而得到BE=CF;
(2)由△BDE≌△CDF,可知∠B=∠C,根据等角对等边可证AB=AC.
解答 证明:(1)∵D是△ABC的BC边的中点,DE⊥AB,DF⊥AC,
∴BD=CD,△BDE、△CDF均为直角三角形;
在Rt△BDE和Rt△CDF中,
$\left\{\begin{array}{l}{BD=CD}\\{DE=DF}\end{array}\right.$,
∴△BDE≌△CDF(HL),
∴BE=CF;
(2)∵△BDE≌△CDF,
∴∠B=∠C,
∴AB=AC.
点评 该题主要考查了全等三角形的判定、等腰三角形的判定等几何知识点及其应用问题;牢固掌握全等三角形的判定、等腰三角形的判定等几何知识点是解题的基础和关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
16.下列图案既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.方程x(x+3)=k(x+3)有一个根为正数,则k满足的条件是( )
| A. | k>0 | B. | k<0 | C. | k≠0 | D. | 以上答案都不对 |
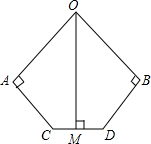 如图,OA=0B,AC=BD,0A⊥AC,0B⊥BD,OM⊥CD于M,求证:OM平分∠A0B.
如图,OA=0B,AC=BD,0A⊥AC,0B⊥BD,OM⊥CD于M,求证:OM平分∠A0B.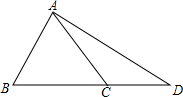 如图,C是△ABD的边BD上的一点,且AC=BC,你能判断AD与BD的大小吗?
如图,C是△ABD的边BD上的一点,且AC=BC,你能判断AD与BD的大小吗?