题目内容
在△ABC中，DE∥BC，且AD：DB=2：1，那么DE：BC等于（ ）| A、2：1 | B、1：2 |
| C、3：2 | D、2：3 |
考点：相似三角形的判定与性质
专题：
分析：利用DE∥BC及AD：DB=2：1，可求出
=
，即可求出DE：BC=2：3．
| AD |
| AB |
| 2 |
| 3 |
解答：解：∵DE∥BC，
∴
=
，
∵AD：DB=2：1，
∴
=
，
∴DE：BC=2：3．
故选：D．
∴
| AD |
| AB |
| DE |
| BC |
∵AD：DB=2：1，
∴
| AD |
| AB |
| 2 |
| 3 |
∴DE：BC=2：3．
故选：D．
点评：本题主要考查了相似三角形的判定与性质，解题的关键是求出
．
| AD |
| AB |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在下列各式中，能因式分解的是（ ）
| A、x2+（-y）2 |
| B、4x2+y2 |
| C、-x2+y2 |
| D、x2-y3 |
已知某三角形的一条边长为a，一条边长为b，则这个三角形面积不可能为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，AB∥CD，∠A、∠P、∠C三个角之间存在怎样的关系？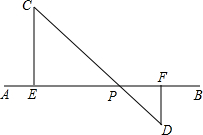
如图，AB是一条河流，要铺设管道将河水引到C、D两个用水点，现有两种铺设管道的方案； 
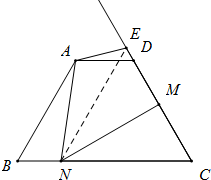已知，在等腰梯形ABCD中，AD∥BC，AD=2，AB=CD=4，且∠B=60°，M是CD上一动点，作MN⊥CD，交BC于N，将∠C沿MN翻折，使点C落在射线CD上的点E处，当△ANE为等腰三角形时，CM的长为