题目内容
11.用适当方法解方程(1)2x2-3x-14=0
(2)(2y-1)2=3(1-2y)
分析 (1)将方程的左边用十字相乘法因式分解后即可转化为一元一次方程求解;
(2)移项后提取公因式即可达到降次的目的,从而求解一元二次方程.
解答 解:(1)方程左边因式分解为(2x-7)(x+2)=0,
即2x-7=0或x+2=0,
解得:${x_1}=\frac{7}{2},{x_2}=-2$;
(2)移项得:(2y-1)2-3(1-2y)=0,
提公因式得:(2y-1)(2y-1+3)=0
即:2y-1=0,2y+2=0,
解得:${y_1}=\frac{1}{2},{y_2}=-1$.
点评 本题考查了因式分解法解一元二次方程,解题的关键是能够将二次三项式进行因式分解,难度不大.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
1.下列公式正确的是( )
| A. | a2=b2+c2+2bccosA | B. | a2=b2+c2+bccosA | ||
| C. | a2=b2+c2-2bccosA | D. | a2=b2+c2-2bcsinA |
19.下列运算可以运用平方差公式的是( )
| A. | (a+1)(a-1) | B. | (2+a)(a+2) | C. | (-a+b)(-a+b) | D. | (a2-b)(a-b2) |
16.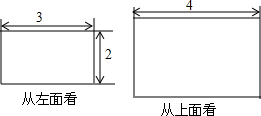 一个长方体从左面看,上面看到的相关数据如图所示,则其从正面看到的图形面积是( )
一个长方体从左面看,上面看到的相关数据如图所示,则其从正面看到的图形面积是( )
 一个长方体从左面看,上面看到的相关数据如图所示,则其从正面看到的图形面积是( )
一个长方体从左面看,上面看到的相关数据如图所示,则其从正面看到的图形面积是( )| A. | 6 | B. | 8 | C. | 12 | D. | 24 |
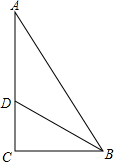 如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BD=10厘米,BC=8厘米,DC=6厘米,则点D到直线AB的距离是6厘米.
如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BD=10厘米,BC=8厘米,DC=6厘米,则点D到直线AB的距离是6厘米.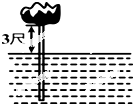 如图,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面3尺.突然一阵大风吹过,红莲被吹至一边,花朵刚好齐及水面,如果知道红莲移动的水平距离为6尺,则水是( )尺.
如图,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面3尺.突然一阵大风吹过,红莲被吹至一边,花朵刚好齐及水面,如果知道红莲移动的水平距离为6尺,则水是( )尺.