题目内容
已知：∠A=∠B，求证：∠C=∠D．考点：三角形内角和定理,对顶角、邻补角
专题：证明题
分析：先根据对顶角相等得出∠AOD=∠BOC，再由∠A=∠B即可得出结论．
解答：
解：∵∠AOD与∠BOC是对顶角，
∴∠AOD=∠BOC，
∵∠A=∠B，∠A+∠D+∠AOD=180°，∠B+∠C+∠BOC=180°，
∴∠C=∠D．
解：∵∠AOD与∠BOC是对顶角，∴∠AOD=∠BOC，
∵∠A=∠B，∠A+∠D+∠AOD=180°，∠B+∠C+∠BOC=180°，
∴∠C=∠D．
点评：本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．
练习册系列答案
相关题目
下列计算正确的是（ ）
| A、（-2）0=0 | ||
| B、3-2=-9 | ||
| C、（a-3）2=a6 | ||
D、a-3=
|
在某市改造的某项目中，要将如图所示的一棵没有观赏价值的树砍倒，栽种其他树木，在操作过程中，甲师傅要直接将树砍倒，乙师傅不同意，他担心这样会损害这棵树周围5m处的花草和动物雕塑，请你根据图中标注的测量数据，通过计算说明乙师傅的担心是否必要．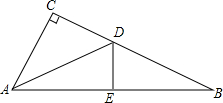
如图，在Rt△ABC中，∠C=90°，AB的垂直平分线与BC，AB的交点分别为D，E．
如图，在正六边形ABCDEF（各边相等，各角相等）中，△DOE可以由
如图，边长为acm的正方体其上下底面的对角线AC、A1C1与平面H垂直．