题目内容
11.已知一次函数y=-x+8和反比例函数y=$\frac{k}{x}$图象在第一象限内有两个不同的公共点A、B,则实数k的取值范围为0<k<16.分析 先由两解析式组成方程组,消去y得到关于x的一元二次方程x2-8x+k=0,根据题意得到此方程有两个不相等的实数根,则△=82-4×k>0,然后解不等式即可;
解答 解:∵一次函数y=-x+8和反比例函数y=$\frac{k}{x}$图象在第一象限内有两个不同的公共点A、B,
∴k>0,
由$\left\{\begin{array}{l}{y=-x+8}\\{y=\frac{k}{x}}\end{array}\right.$得-x+8=$\frac{k}{x}$,
整理得x2-8x+k=0,
∵方程组有两组解,
∴△=82-4×k>0,
∴k<16,
故答案为0<k<16.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 第一次模拟考试后,数学老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到后第二、三、四组的频数比为3:10:8,然后请学生(也请你一起)结合统计图完成下列问题:
第一次模拟考试后,数学老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到后第二、三、四组的频数比为3:10:8,然后请学生(也请你一起)结合统计图完成下列问题: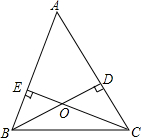 如图,在△ABC中,BD⊥AC,CE⊥AB,垂足分别为D、E,BD、CE相交于点O.
如图,在△ABC中,BD⊥AC,CE⊥AB,垂足分别为D、E,BD、CE相交于点O.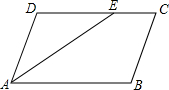 如图,已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD,AB于E,F.
如图,已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD,AB于E,F.