题目内容
5.某乡镇计划购买A、B两种树苗共100棵,A种树苗每棵30元,B种树苗每棵90元(1)设购买A种树苗x棵,购买A、B两种树苗总费用y元,写出y与x之间的函数关系式;
(2)购买A、B树苗的总费用不超过7560元,且B是A的是3倍,有几种购买方案?
(3)哪种方案更合算.
分析 (1)设购买A种树苗x棵,购买A、B两种树苗的总费用为y元,根据某乡镇计划购买A、B两种树苗共100棵,已知A种树苗每棵30元,B种树苗每棵90元可列出函数关系式.
(2)根据购买A、B两种树苗的总费用不超过7560元,且B种树苗的棵树不少于A种树苗棵树的3倍,列出不等式组,解不等式组即可得出答案;
(3)根据(1)得出的y与x之间的函数关系式,利用一次函数的增减性结合自变量的取值即可得出更合算的方案.
解答 解:(1)设购买A种树苗x棵,购买A、B两种树苗的总费用为y元,
y=30x+90(100-x)=9000-60x;
(2)设购买A种树苗x棵,则B种树苗(100-x)棵,根据题意得:
$\left\{\begin{array}{l}{9000-60x≤7560}\\{100-x≥3x}\end{array}\right.$,
解得:24≤x≤25,
因为x是正整数,
所以x只能取25,24.
有两种购买树苗的方案:
方案一:购买A种树苗25棵时,B种树苗75棵;
方案二:购买A种树苗24棵时,B种树苗76棵;
(3)∵y=9000-60x,-60<0,
∴y随x的增大而减小,
又x=25或24,
∴采用购买A种树苗25棵,B种树苗75棵时更合算.
点评 本题考查的是一元一次不等式组及一次函数的应用,解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系和不等关系.

练习册系列答案
相关题目
14.-8的立方根是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | $\sqrt{2}$ |
15.某药品经过两次降价,每瓶零售价由180元降为100元.已知两次降价的百分率相同,设每次降价的进分率为x,根据题意列方程正确的是( )
| A. | 180(1+x)2=100 | B. | 180(1-x2)=100 | C. | 180(1-2x)=100 | D. | 180(1-x)2=100 |
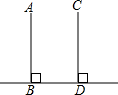 如图,如果直线AB⊥BD,CD⊥BD,B、D为垂足,那么直线AB和CD平行吗?为什么?由此你能得到什么结论?
如图,如果直线AB⊥BD,CD⊥BD,B、D为垂足,那么直线AB和CD平行吗?为什么?由此你能得到什么结论?
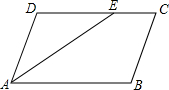 如图,已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD,AB于E,F.
如图,已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD,AB于E,F. 如图,一根木棍OE垂直平分柱子AB,AB=200cm,OE=260cm,一只小猫C由柱子底端A点以2cm/s的速度向顶端B点爬行,同时,另一只小猫D由O点以3cm/s的速度沿木棍OE爬行.问:是否存在这样的时刻,使两只小猫与O点组成的三角形面积是1800cm2?
如图,一根木棍OE垂直平分柱子AB,AB=200cm,OE=260cm,一只小猫C由柱子底端A点以2cm/s的速度向顶端B点爬行,同时,另一只小猫D由O点以3cm/s的速度沿木棍OE爬行.问:是否存在这样的时刻,使两只小猫与O点组成的三角形面积是1800cm2?