题目内容
已知在△ABC中，∠C=90°，AB=15，AC：BC=3：4，则BC= ．
考点：勾股定理
专题：
分析：根据比例设AC=3k，BC=4k（k＞0），然后利用勾股定理列出方程求出k，从而得解．
解答：解：∵AC：BC=3：4，
∴设AC=3k，BC=4k（k＞0），
由勾股定理得，AC2+BC2=AB2，
即（3k）2+（4k）2=152，
解得k=3，
所以BC=4×3=12．
故答案为：12．
∴设AC=3k，BC=4k（k＞0），
由勾股定理得，AC2+BC2=AB2，
即（3k）2+（4k）2=152，
解得k=3，
所以BC=4×3=12．
故答案为：12．
点评：本题考查了勾股定理，利用“设k法”求解更简便．
练习册系列答案
相关题目
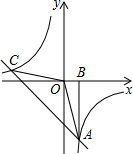如图，已知正比例函数y=kx的图象与反比例函数y=