Question

2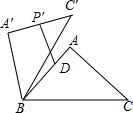．如图，将锐角△ABC绕点B逆时针旋转α（其中0°＜α≤360°），得到△A′BC′，点D是边AB的中点，点P是边AC（含端点）上的一个动点，在△ABC绕点B逆时针旋转的过程中，点P的对应点是点P′．若AB=10，AC=8$\sqrt{2}$，∠ACB=45°，DP′的长度为x，则x的取值范围是7$\sqrt{2}$-5≤x≤19．

Answer 1

分析 由于D为AB的中点，P′为动点，则当DP⊥A′C′时，DP′最短，而在△ABC绕点B逆时针旋转（0°＜a≤360°）的过程中，当DP′在直线AB上时，DP′最短，然后根据旋转的性质得到∠C′=∠C=45°，BC′=BC=14，再利用含45度的直角三角形三边的关系得到BP′=7$\sqrt{2}$，而BD=5，所以DP′=BP₁-BD=7$\sqrt{2}$-5，当D、B、P′在一条直线上，且P′在点C′处时，DP′最长，此时BP′=14，BD=5，则BP′=14+5=19，从而求得x的取值范围是7$\sqrt{2}$-5≤x≤19．

解答 解：过A点作AE⊥BC于E，
∵AB=10，AC=8$\sqrt{2}$，∠ACB=45°，
∴AE=CE=$\frac{\sqrt{2}}{2}$AC=8，
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=6，
∴BC=14，
∵D为AB的中点，P′为动点，
∴当DP′⊥A′C′时，DP′最短，
∵在△ABC绕点B逆时针旋转a角（0°＜a≤360°）的过程中，当DP′在直线AB上，且P′点为A′C′与AB垂直时的垂足时，DP′最短，如图1，
∵△ABC绕点B逆时针旋转a角（0°＜a≤360°）得到△A′BC′，
∴∠C′=∠C=45°，BC′=BC=14，
∴BP′=$\frac{\sqrt{2}}{2}$BC′=7$\sqrt{2}$，
∵AB=10，D为AB的中点，
∴BD=5，
∴P′D=BP′-BD=7$\sqrt{2}$-5．
∵在△ABC绕点B逆时针旋转a角（0°＜a≤360°）的过程中，当D、B、P′在一条直线上，且P′在点C′处时，DP′最长，如图2，
∵BC′=BC=14，
∴BP′=14，
∵BD=5，
∴BP′=14+5=19，
∴7$\sqrt{2}$-5≤x≤19．
故答案为7$\sqrt{2}$-5≤x≤19．

点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．