题目内容
20.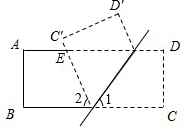 如图,长方形纸片CD沿MN折叠(M,N在AD、BC上),AD∥BC,C′,D′为C、D的对称点,C′N交AD于E.
如图,长方形纸片CD沿MN折叠(M,N在AD、BC上),AD∥BC,C′,D′为C、D的对称点,C′N交AD于E.(1)若∠1=62°,则∠2=56°;
(2)试判断△EMN的形状,并说明理由.
分析 (1)由折叠的性质得:∠ENM=∠1=62°,由平角定义即可得出结果;
(2)由折叠的性质和平行线的性质得出∠MNE=∠EMN,证出EN=EM即可.
解答 解: (1)如图所示:由折叠的性质得:∠MNE=∠1=62°,
(1)如图所示:由折叠的性质得:∠MNE=∠1=62°,
∴∠2=180°-2×62°=56°;
故答案为:56°;
(2)△EMN为等腰三角形;理由如下:
由折叠的性质知:∠1=∠MNE,
又AD∥BC,
∴∠1=∠EMN,
∴∠MNE=∠EMN,
∴EN=EM,
即△EMN为等腰三角形.
点评 本题考查了折叠变换的性质、矩形的性质、平行线的性质、等腰三角形的判定等知识;熟练掌握折叠变换和矩形的性质是解决问题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
15. 如图是一个五角星图案,则∠A+∠B+∠C+∠D+∠E的度数是( )
如图是一个五角星图案,则∠A+∠B+∠C+∠D+∠E的度数是( )
 如图是一个五角星图案,则∠A+∠B+∠C+∠D+∠E的度数是( )
如图是一个五角星图案,则∠A+∠B+∠C+∠D+∠E的度数是( )| A. | 180° | B. | 150° | C. | 135° | D. | 120° |
9.某汽车销售店计划上半年每月销售20辆汽车,由于某种原因未能按计划执行,实际每月的销售情况如下表(规定比计划月销售量增加为正,减少为负):
(1)请把上表补充完整;
(2)销量最多的一个月比销量最少的一个月多销售多少辆?
(3)这半年内总销量比原计划多了还是少了?多或少了多少辆?
(4)这半年内实际平均每月销售了多少辆汽车?
| 月份 | 一 | 二 | 三 | 四 | 五 | 六 |
| 实际月销售(辆) | 24 | 19 | 22 | 23 | ||
| 比计划月销售量增(辆) | +4 | -2 | 0 | +3 |
(2)销量最多的一个月比销量最少的一个月多销售多少辆?
(3)这半年内总销量比原计划多了还是少了?多或少了多少辆?
(4)这半年内实际平均每月销售了多少辆汽车?
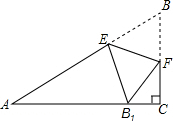 如图,在△ABC中,∠C=90°,点E,F分别在边AB,BC上,沿直线EF将△EBF翻折,使顶点B的对应点B1落在AC边上,且EB1⊥AC.求证:四边形BFB1E是菱形.
如图,在△ABC中,∠C=90°,点E,F分别在边AB,BC上,沿直线EF将△EBF翻折,使顶点B的对应点B1落在AC边上,且EB1⊥AC.求证:四边形BFB1E是菱形. 已知,如图,以矩形ABCD的一边CD为边向外作等边△PCD,请你用无刻度的直尺作出线段AB的垂直平分线(保留作图痕迹)
已知,如图,以矩形ABCD的一边CD为边向外作等边△PCD,请你用无刻度的直尺作出线段AB的垂直平分线(保留作图痕迹)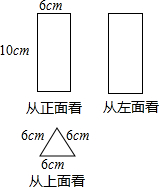 如图是从不同方向看一个几何体得到的形状图及部分数据:
如图是从不同方向看一个几何体得到的形状图及部分数据: 如图,平行四边形ABCD中,∠ABC=75°,AF⊥BC,垂足为F,AF交BD于E,若DE=2AB,求∠AED的度数.
如图,平行四边形ABCD中,∠ABC=75°,AF⊥BC,垂足为F,AF交BD于E,若DE=2AB,求∠AED的度数.