题目内容
3.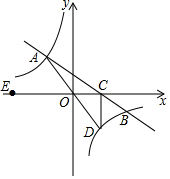 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(12,n)
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(12,n),OA=10,E为x轴负半轴上一点,且tan∠AOE=$\frac{4}{3}$.
(1)求该反比例函数和一次函数的解析式;
(2)延长AO交双曲线于点D,连接CD,求△ACD的面积.
分析 (1)根据OA=10,tan∠AOE=$\frac{4}{3}$,即可得到A(-6,8),进而得出反比例函数解析式为:y=-$\frac{48}{x}$,根据A(-6,8),B(12,-4),利用待定系数法即可得出一次函数的解析式为y=-$\frac{2}{3}$x+4;
(2)先求得C(6,0),D(6,-8),再根据S△ACD=S△ACO+S△CDO进行计算即可.
解答 解:(1)如图,过A作AF⊥x轴于F,
∵OA=10,tan∠AOE=$\frac{4}{3}$,
∴可设AF=4a,OF=3a,则由勾股定理可得:
(3a)2+(4a)2=102,
解得a=2,
∴AF=8,OF=6,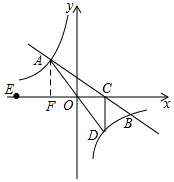
∴A(-6,8),
代入反比例函数y=$\frac{m}{x}$,可得m=-48,
∴反比例函数解析式为:y=-$\frac{48}{x}$,
把点B(12,n)代入y=-$\frac{48}{x}$,可得n=-4,
∴B(12,-4),
设一次函数的解析式为y=kx+b,则
$\left\{\begin{array}{l}{8=-6k+b}\\{-4=12k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{2}{3}}\\{b=4}\end{array}\right.$,
∴一次函数的解析式为y=-$\frac{2}{3}$x+4;
(2)在一次函数y=-$\frac{2}{3}$x+4中,令y=0,则x=6,即C(6,0),
∵A(-6,8)与点D关于原点成中心对称,
∴D(6,-8),
∴CD⊥x轴,
∴S△ACD=S△ACO+S△CDO
=$\frac{1}{2}$CO×AF+$\frac{1}{2}$CO×CD
=$\frac{1}{2}$×6×8+$\frac{1}{2}$×6×8
=48.
点评 本题主要考查了反比例函数与一次函数交点问题,解题时注意:反比例函数与一次函数交点坐标同时满足反比例函数与一次函数解析式.解决问题的关键是作辅助线构造直角三角形.

 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案| A. | 4和5 | B. | 5和6 | C. | 6和7 | D. | 7和8 |
| A. | 了解我国青年人喜欢的电视节目应采用全面调查 | |
| B. | 对飞机乘客的安检应采用抽样调查 | |
| C. | “掷一次硬币,出现正面向上”是随机事件 | |
| D. | “购买1张彩票就中奖”是不可能事件 |
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
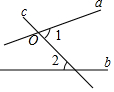 如图,直线a,b被直线c所截,记a与c的交点为O,且∠1=65°,∠2=45°,若要使a∥b,则a需绕点O( )
如图,直线a,b被直线c所截,记a与c的交点为O,且∠1=65°,∠2=45°,若要使a∥b,则a需绕点O( )| A. | 逆时针旋转25° | B. | 逆时针旋转20° | C. | 顺时针旋转25° | D. | 顺时针旋转20° |
 如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若斜坡AF的坡度i=1:$\sqrt{3}$,则大树的高度为( )(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,$\sqrt{3}$≈1.732)
如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若斜坡AF的坡度i=1:$\sqrt{3}$,则大树的高度为( )(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,$\sqrt{3}$≈1.732)