先化简.再求值:$\frac{{x}^{2}+2x+1}{{x}^{2}-1}$-$\frac{x}{x-1}$.其中x=3．题目和参考答案——青夏教育精英家教网—

题目内容

14．先化简，再求值：$\frac{{x}^{2}+2x+1}{{x}^{2}-1}$-$\frac{x}{x-1}$，其中x=3．

分析首先分解因式，进而利用分式混合运算法则求出答案．

解答解：$\frac{{x}^{2}+2x+1}{{x}^{2}-1}$-$\frac{x}{x-1}$
=$\frac{（x+1）^{2}}{（x+1）（x-1）}$-$\frac{x}{x-1}$
=$\frac{x+1}{x-1}$-$\frac{x}{x-1}$
=$\frac{1}{x-1}$，
把x=3代入得：
原式=$\frac{1}{3-1}$=$\frac{1}{2}$．

点评此题主要考查了分式的化简求值，正确掌握运算法则是解题关键．

练习册系列答案

相关题目

4．

如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上的一点，点E在BC边上，连接AE、DE、DC，AE=CD．求证：∠BAE=∠BCD．

5．

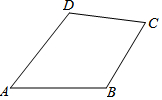如图，在四边形ABCD中，AB=AD，CB=CD．请你添加一条线把它分成两个全等三角形，并给出证明．

2．某网店店主购进A，B两种型号的装饰链，其中A型装饰链的进货单价比B型装饰链的进货单价多20元，花500元购进A型装饰链的数量与花400元购进B型装饰链的数量相等．销售中发现A型装饰链的每月销量y₁（个）与销售单价x（元）之间满足的函数关系式为y₁=-x+200；B型装饰链的每月销售y₂（个）与销售单价x（元）之间的关系满足一次函数关系y₂=-x+140．
（1）求A，B两种型号装饰链的进货单价．
（2）直接写出B型装饰链的每月销量y₂（个）与销售单价x（元）之间的函数关系式为y₂=-x+140．
（3）已知每个A型装饰链的销售单价比B型装饰链的销售单价高20元．求A，B两种型号装饰链的销售单价各为多少元时，每月销售这两种装饰链的总利润最大，最大总利润是多少？

9．（1）计算：|-3|+$\sqrt{3}$tan30°-$\sqrt{12}$-（2016-π）⁰
（2）先化简，再求值：$\frac{2a+1}{{a}^{2}-1}$•$\frac{{a}^{2}-2a+1}{{a}^{2}-a}$-$\frac{1}{a+1}$，其中a=-$\frac{1}{2}$．

19．地球的平均半径约为6 371 000米，该数字用科学记数法可表示为6.371×10⁶．

6．若分式$\frac{x+3}{x-3}$的值为零，则x的值为-3．

3．

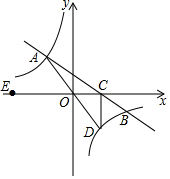如图，在平面直角坐标系xOy中，一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$（m≠0）的图象交于二、四象限内的A、B两点，与x轴交于C点，点B的坐标为（12，n）
，OA=10，E为x轴负半轴上一点，且tan∠AOE=$\frac{4}{3}$．
（1）求该反比例函数和一次函数的解析式；
（2）延长AO交双曲线于点D，连接CD，求△ACD的面积．

4．如果点（a，b）为正比例函数y=（2m-1）x的图象上任意一点，且a+b=0，那么m的值是（　　）

试题分类