题目内容
14. 如图,直线y=kx+8分别与x轴,y轴相交于A,B两点,O为坐标原点,A点的坐标为(4,0).
如图,直线y=kx+8分别与x轴,y轴相交于A,B两点,O为坐标原点,A点的坐标为(4,0).(1)求k的值;
(2)过线段AB上一点P(不与端点重合)作x轴,y轴的垂线,垂足分别为M,N.当矩形PMON的面积是6时,求点P的坐标.
分析 (1)因为直线y=kx+8分别与x轴,y轴相交于A,B两点,O为坐标原点,A点的坐标为(4,0),即直线y=kx+8经过A(4,0),所以0=4k+8,解之即可;
(2)因为四边形PNOM是矩形,点P在直线y=-2x+8上,设P(t,-2t+8),则PN=t,M=-2t+8,而S=PN•PM=6,由此即可得到关于t的方程,解方程即可求得.
解答 解:(1)∵直线y=kx+8经过A(4,0),
∴0=4k+8,
∴k=-2.
(2)∵点P在直线y=-2x+8上,设P(t,-2t+8),
∴PN=t,PM=-2t+8,
∵四边形PNOM是矩形,
∴S=t•(-2t+8)=6,
即-2t2+8t=6,
解得t1=1,t2=3,
∴点P的坐标为(1,6)或(3,2).
点评 本题考查了一次函数图象上点的坐标特征,数形结合、方程和转化等数学思想方法是解题的关键.

练习册系列答案
相关题目
4.某商场举办“迎新春送大礼”的促销活动,全场商品一律打八折销售.王老师买了一件商品,比标价少付了50元,那么他购买这件商品花了( )
| A. | 100元 | B. | 150元 | C. | 200元 | D. | 250元 |
5. 对某班学生一次体育项目达标测试成绩进行统计分析,各等级的人数如图所示:
对某班学生一次体育项目达标测试成绩进行统计分析,各等级的人数如图所示:
(1)根据图中数据填写下表
(2)请计算各等级的频率之和为1,你认为这个结果是必然发生的事吗?不是(答“是”或“不是”).
 对某班学生一次体育项目达标测试成绩进行统计分析,各等级的人数如图所示:
对某班学生一次体育项目达标测试成绩进行统计分析,各等级的人数如图所示:(1)根据图中数据填写下表
| 等级 | 差 | 中 | 良 | 优 |
| 频数 | 6 | 12 | 24 | 18 |
| 频率 | 10% | 20% | 40% | 30% |
9.给出下列式子:0,3a,π,$\frac{x-y}{2}$,1,3a2+1,$-\frac{xy}{11}$,$\frac{1}{x}+y$.其中单项式的个数是( )
| A. | 5个 | B. | 1个 | C. | 2个 | D. | 3个 |
19.某学校开展“文明礼仪”演讲比赛,八(1)、八(2)班派出的5名选手的比赛成绩如图所示:

(1)填表:
(2)根据题中数据计算八(2)班成绩的方差为160,请计算八(1)班成绩的方差,判断哪个班级选手的成绩更为稳定?并说明理由.

(1)填表:
| 平均数(分) | 中位数(分) | 众数(分) | |
| 八(1)班 | 75 | 75 | 75 |
| 八(2)班 | 75 | 70 | 90 |
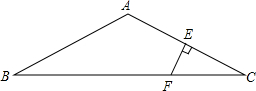 如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明.
如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明. 如图所示,直线l1与l2相交于点O,且∠1+∠3=2(∠2+∠4),求下列角的度数.
如图所示,直线l1与l2相交于点O,且∠1+∠3=2(∠2+∠4),求下列角的度数. 如图,直径AB和弦CD相交,若弧AC和弧BC的度数比是2:1,D是弧AB中点,则∠OCD的度数是15度.
如图,直径AB和弦CD相交,若弧AC和弧BC的度数比是2:1,D是弧AB中点,则∠OCD的度数是15度. 在锐角三角形ABC中,AB=6,AD是BC边上的高,BD=3,AC=3$\sqrt{6}$,求∠C的度数.
在锐角三角形ABC中,AB=6,AD是BC边上的高,BD=3,AC=3$\sqrt{6}$,求∠C的度数.